Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Восточно–Сибирский государственный

Университет технологий и управления»

(ФГБОУ ВПО ВСГУТУ)

Изучение электромагнитных затухающих колебаний

Методическое указание к лабораторной работе

Составители: Санеев Э.Л.

Манжуев В.М.

Шагдаров В.Б.

Улан-Удэ

Издательство ВСГУТУ

2011

В лабораторной работе изучаются свободные электромагнитные затухающие колебания при помощи осциллографа. По результатам работы строится зависимость логарифмического декремента затухания от сопротивления контура, по которой находится сопротивление катушки. Определяется активное сопротивление контура. Рассчитывается добротность контура.

1. Теоретическое введение

1.1.Общие положения.

Свободными затухающими колебаниями называются колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается. Закон, по которому происходят колебания, зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса.

Линейными системами являются, к примеру, пружинный маятник при малых деформациях пружины, колебательный контур индуктивность, ёмкость и сопротивление которого не зависит ни от тока в контуре, ни от напряжения.

Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

(1.1)

где s - колеблющаяся величина, β = const - коэффициент затухания, ω₀ - циклическая частота свободных незатухающих колебаний той же колебательной системы при отсутствии потерь энергии (при β = 0) называется собственной частотой колебательной системы.

При не слишком сильном затухании (при β < ω₀) общее решение уравнения (1.1) имеет вид:

(1.2)

где A₀ и φ - произвольные постоянные, ω- величина, определяемая формулой:

. (1.3)

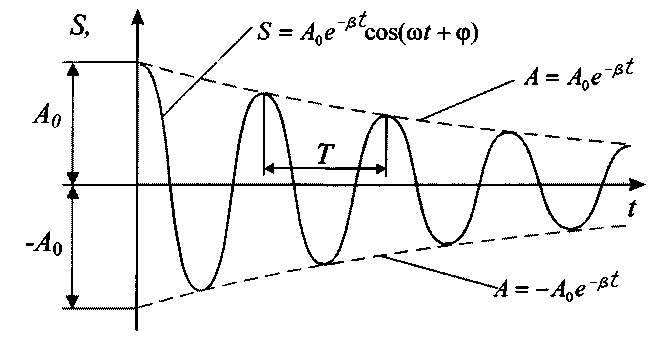
На рисунке 1 дан график функции (1.2). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки s.

Рис.1 График функции

В соответствии с видом функции (1.2) движение системы можно рассматривать как гармоническое колебание частоты с амплитудой, изменяющейся по закону:

.

Верхняя из пунктирных кривых дает график функции A(t), причем величина А₀ представляет собой амплитуду в начальный момент времени.

Период затухания колебаний равен:

При незначительном сопротивлении среды (β < ω₀) период колебаний практически не изменяется и равен

.

Последующие наибольшие отклонения в какую–либо сторону (например, и т.д. на рис.) образуют геометрическую прогрессию. Действительно, если , то , и т.д.

Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

Это соотношение называется декрементом затухания, а его натуральный логарифм – логарифмическим декрементом затухания.

Для характеристики колебательной системы обычно используется логарифмический декремент затухания. Выразив β через δ и Т, можно закон убывания амплитуды со временем записать в виде:

.

Таким образом, величина δ определяет степень убывания амплитуды в течение одного периода.

Важной характеристикой колебательной системы является добротность Q - безразмерная величина, равная произведению 2π на отношение энергии W(t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до (t + Т), то есть за один период колебания:

Так как энергия W(t) пропорциональна квадрату амплитуды колебаний A(t), то

При малых значениях логарифмического декремента затухания (δ <<1) [1 – еxp(-2δ) ≈ 2δ] и добротность колебательной системы

(1.4)

(T принято равным Т₀, так как затухание невелико (β << ω₀)).