3.2 Нечеткое включение и равенство множеств. Нечеткое бинарное отношение.
Понятие нечеткого включения и равенств множеств, нечеткого бинарного отношения являются одними из основных понятий процесса принятия решений при наличии экспертной информации.
Пусть и – нечеткие множества.
Степенью
включения
множества
в
называется величина
( , )= & (А1(х) А2(х)). (21)
х Х
Операция есть импликация, определяемая как:
А1(х) А2(х)= 1& (1 - А1(х) + А2(х))= min 1, 1 - А1(х) + А2(х).
Степенью равенства нечетких множеств и называется величина ( , ), определяемая как логическая сумма эквивалентностей.
( , ) = & (µА1(х) А2(х)). (22)
х Х
Здесь операция эквивалентности:
А1(х) А2(х) = (А1(х) А2(х)) & (А2(х) А1(х)).
Очевидно, что ( , ) = ( , ) & ( , ).
Степень включения и степень равенства могут принимать любые значения из отрезка [0,1].
Пример 6: Даны нечеткие множества
= 0.3/х2 , 0.6/х3 , 0.4/х5>,
= 0.8/х1, 0.5/х2 , 0.7/х3 , 0.6/х5 ,
определённые на универсальном множестве Х=х1,х2,х3,х4,х5.
Определим степень включения множества в (( , )) и множества и (( , )).
( , ) = ( 0 - 0.8) & (0.3 - 0.5) & (0.6 - 0.7) & (0 - 0) & (0.4 - 0.6) = (1&(1- 0 + 0.8)) & (1&(1- 0.3 + 0.5)) & (1&(1- 0.6 + 0.7)) & (1&(1- 0 + 0)) & (1&(1- 0.4 + 0.6)) = 1 & 1 & 1 & 1 & 1 = 1
( , )= (0.8 - 0) & (0.5 - 0.3) & (0.7 - 0.6) & (0 - 0) & (0.6 - 0.4) = (1&(1- 0.8 + 0)) & (1&(1- 0.5 + 0.3)) & (1&(1- 0.7 + 0.6)) & (1&(1- 0 + 0)) & (1&(1- 0.6 + 0.4)) = 0.2 & 0.8 & 0.9 & 1 & 0.8 = 0.2
Тогда степень равенства множеств и будет равна 0.2.
Нечетким
бинарным отношением
на множестве Х называется нечеткое
множество вида:
,
где хi, хj – некоторая пара элементов из
множества Х; (хi,
хj) – функция принадлежности, определяемая
субъективной мерой того, насколько пара
(хi, хj) соответствует бинарному отношению
.
Если множество Х конечно (счетно) и невелико, то нечеткое бинарное отношение удобно представить в виде матрицы М(R). Матрица М – квадратная с числом строк и столбцов, равным количеству элементов множества Х. В матрице строки и столбцы помечаются элементами множества Х. В сроке, соответствующей элементу хi на пересечении её со столбцом, соответствующим элементу хj, располагается значение функции принадлежности (хi, хj).
Пример 7: Пусть Х = 1,3,5,7,9. Определить на множестве Х нечеткое бинарное отношение намного больше. Тогда матрица М(R) может иметь вид:
.
(23)
3.3 Нечеткая и лингвистическая переменные.
Понятие нечеткой и лингвистической переменной используется экспертом при описании сложных объектов и явлений, а также при формализации процессов принятия решений на трудно формализуемых этапах проектирования.
Нечеткой переменной называется тройка объектов вида:
, Х, С, (24)
где –наименование нечеткой переменной, Х=х-область её определения,
С= (х)/х - нечеткое множество на Х, описывающее ограничения на возможные значения нечеткой переменной (т.е. её семантику).
Лингвистической переменной называется пятёрка объектов:
, Т, Х, G, М, (25)
где – наименование лингвистической переменной, Т – множество её значений (терм - множество), нечеткие переменные, областью определения каждой из которых является множество Х, G – синтаксическая процедура, позволяющая оперировать элементами терм - множества Т, в частности генерировать новые осмысленные термы (при традиционном подходе процедура G определяет новые значения лингвистической переменной, исходя из её базового терм – множества Т и логических операций И, ИЛИ, НЕ, ОЧЕНЬ, СЛЕГКА), М – семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную путём формирования соответствующего нечеткого множества. Например, семантические процедуры могут иметь вид:
М(
ИЛИ
)
=
–
объединение нечетких множеств
М(
И
)
=
– пересечение нечетких множеств
М(НЕ
)
=
– дополнение нечетких множеств
М(ОЧЕНЬ ) = CON( ) – концентрация нечетких множеств
М(СЛЕГКА ) = DIL( ) – растяжение нечетких множеств
где
И
– нечеткие множества, соответствующие
нечетким переменным 1
и 2
рассматриваемой лингвистической
переменной.
Пример 8: Пусть эксперт оценивает толщину выпускаемого изделия с помощью понятий: малая толщина, средняя толщина, большая толщина; при этом минимальная толщина изделия равна 10 мм, а максимальная – 80 мм.
Формализация такого описания может быть проведена с помощью лингвистической переменной:
, Т, Х, G, М ,
где – «толщина изделия»; Т = 1, 2, 3 = малая, средняя, большая; Х = [10,80].
Пусть нечеткие множества С1, С2, С3 описывают семантику базовых значений переменной . Функции принадлежности представлены на рис. 10.
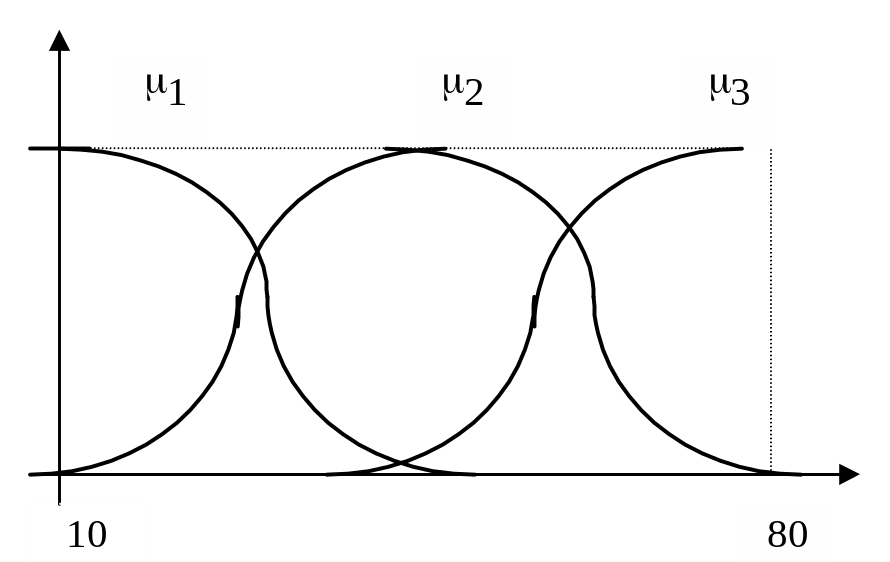
Рисунок 10
Тогда, например, значения 1 = малая или средняя толщина , будет определяться нечетким множеством C1, т.е С1 = М(1 ИЛИ 2) = С1 С2 , функция принадлежности которой имеет вид, представленный на рис. 11.
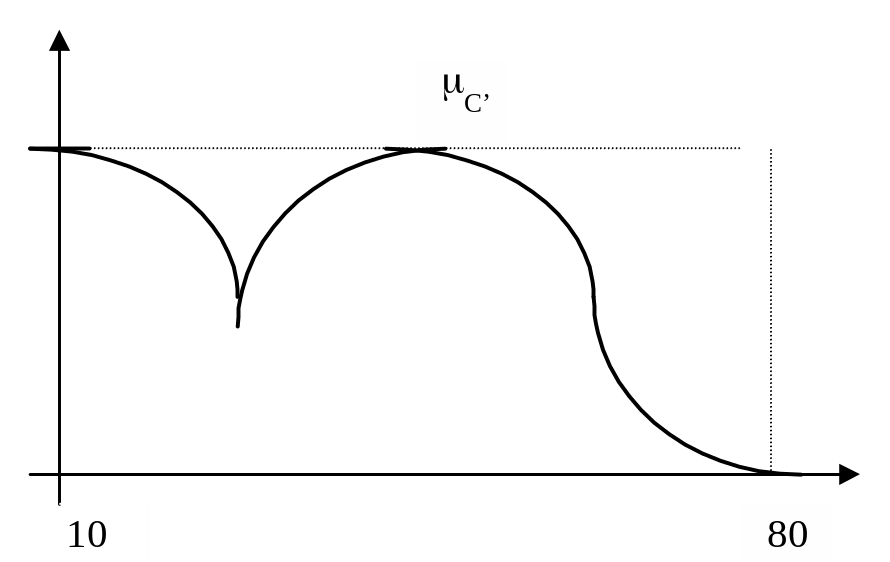
Рисунок 11
А, например значение 2=небольшая толщина будет определяться нечетким множеством С2 ( С2=М(НЕ 3) = С3), функция принадлежности которой имеет вид, представленный на рис. 12.
Рисунок 12
Лингвистическая переменная, у которой процедура образования нового значения G зависит от множества базовых терм – значений Т называется синтаксически зависимой лингвистической переменной.
Наряду с рассмотренными выше синтаксически зависимыми лингвистическими переменными существуют переменные, у которых процедура образования новых значений зависит не от множества базовых терм – значений Т, а от области определения Х (универсальное множество), т. е. G = G(Х). Например, значение лингвистической переменной толщина изделия может быть определено как близкое к 20 мм или приблизительно к 75 мм. Такие лингвистические переменные называются синтаксически независимыми.
Произвольные значения синтаксически независимой лингвистической переменной взаимно однозначно определяется некоторыми значениями х области определения Х. Поэтому произвольное значение (нечеткую переменную ) синтаксически независимой лингвистической переменной задаётся в виде тройки объектов:
= х, Х, С. (26)
Например, нечеткая переменная , определённая как приблизительно 75 мм, запишется в виде: = 75, [10,80], С .