4.6 Выбор значений параметров на основе нечеткой индуктивной схемы вывода

Нечеткой индуктивной схемой вывода называется схема:

(64)

Для системы нечетких высказываний второго типа индуктивная схема вывода принимает вид:

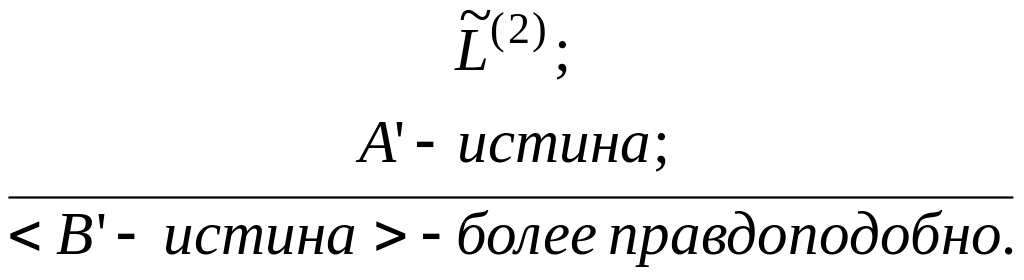(65)

где А=<_W есть w’>, B=<_v есть v’>- четкие высказывания о значении обобщенного входного и выходного параметров.

Истинность данной схемы определяется как:

,

где

(66)

Величина (66) называется степенью истинности индуктивной схемы вывода для нечеткой системы высказываний второго типа. Данное понятие отражает степень соответствия четкого значения v’ выходного параметра V четкому значению w’ обобщенного входного параметра W при задании экспертной информации системой нечетких высказываний второго типа.

Тогда математическая постановка задачи выбора выходного параметра имеет вид:

Найти такие значения выходного параметра V₀, для которых степень истинности (66) схемы (65) на основе нечеткой индуктивной схемы вывода будет максимальной.

5. Выбор варианта

В раздела 4.2, 4.3 рассматривались задачи выбора значений параметров объекта. Другим типом задач является выбор некоторого варианта из заранее заданного, достаточно небольшого числа вариантов. В этом случае экспертная информация может быть представлена в одним из следующих способов:

(67)

или

(68)

Здесь высказывания В_j выражают суть выбора того или иного варианта проектирования, то есть являются четкими высказываниями:

, где v_j – четкое значение из конечного множества вариантов.

1. Выбор варианта при дедуктивном выводе

В этом случае схема вывода имеет вид:

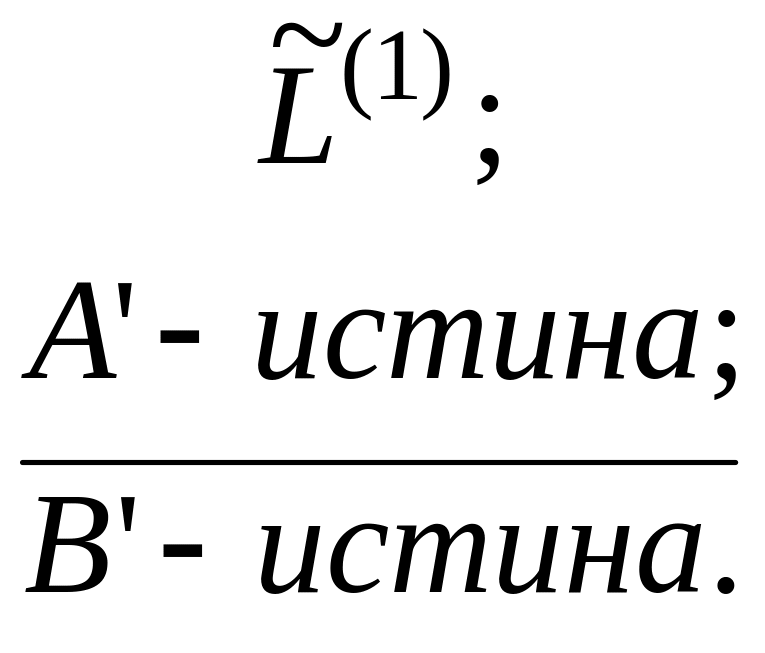(69)

Степень истинности данной схемы для произвольного j-го высказывания системы (65) определяется:

(70)

При этом учитываем, что B_j – четкие высказывания и, следовательно:

(71)

Для выбора варианта v₀V на основе правила modus ponens необходимо:

1. Для каждого v_jV (j=1…m) определить степень истинности по формуле (70);

2. В качестве решения (v₀) выбрать такое v_jV, при котором степень истинности (70) имеет максимальное значение.

4.7.2 Выбор варианта при индуктивном выводе в этом случае используется экспертная информация в виде (68).

Индуктивная схема вывода имеет вид:

(72)

Для выбора варианта проектирования на основе правила modus ponens преобразуем систему (68) второго типа в систему первого типа, согласно правилу контрапозиции (52):

(73)

где ,

, .

Значения и характеризуются функциями принадлежности:

и

Задача принятия решения, как и ранее заключается в выборе такого варианта, при котором степень истинности нечеткого правила modus ponens имеет наибольшее значение.

Для произвольного варианта v_jV степень истинности имеет вид:

Таким образом, в качестве варианта выбирается такой вариант v_kV, для которого степень истинности имеет наибольшее значение, то есть:

_. (74)