3.4.1 Построение функций принадлежности на счетном множестве точек на основе экспертных оценок.

Простейший способ построения функций принадлежности предполагает опрос нескольких экспертов.

Пусть имеется m экспертов, часть которых на вопрос о принадлежности элемента хХ нечеткому множеству А отвечает положительно. Обозначим их число через n1. Другая часть экспертов (n2=m-n1) отвечает на вопрос отрицательно. Тогда функция принадлежности принимается: _А(х) = n1/(n1+n2).

Пример 9: Пусть имеется множество Х: Х = 1, 2, 3, 4, 5

Требуется построить нечеткое множество А, которое формализует нечеткое понятие немного больше двух.

Пусть имеется шесть экспертов. Результаты их опроса имеют вид:

m	x
	1	2	3	4	5
N1	0	0	6	4	1
N2	6	6	0	2	5
	А(1)=0	А(2)=0	А(3)=1	А(4)=0.7	А(5)=0.2

Тогда нечеткое множество А имеет вид:

= 0/1, 0/2, 1/3, 0.7/4, 0.2/5.

Необходимо отметить, что данная схема определения функции принадлежности самая простая, но и самая грубая.

Более точно функцию принадлежности можно построить на основе количественного парного сравнения степеней принадлежности. Такая схема допускает и одного эксперта.

Результатом опроса эксперта является матрица М =||m_ij||,

i,j=1,…n, где n– число точек, в которых сравниваются значения функции принадлежности. Число m_ij показывает, во сколько раз, по мнения эксперта, степень принадлежности _А(х_i) больше _А(х_j). При этом количество вопросов, на которые надо ответить эксперту составляет не n², а лишь (n² - n)/2, так как по определению m_ii =1 и m_ij=1/m_ji.

При этом эксперт оперирует следующими понятиями, представленными в таблице 2.

Таблица 2

Смысл	Mij
(хi) равна (хj)	1
(хi) немного больше (хj)	3
(хi) больше (хj)	5
(хi) заметно больше (хj)	7
(хi) намного больше (хj)	9
Значения, промежуточные по степени между перечисленными	2, 4, 6, 8

Далее, определить значение функции принадлежности _А в точках х1, х2, … хn можно, используя формулу:

(27)

где j – произвольный столбец матрицы М.

Пример 10: Пусть для описания расстояния между двумя точками используется лингвистическая переменная  - расстояние с множеством базовых значений Т = малое, среднее, большое.

Базовое множество лингвистической переменной : Х = 1, 3, 6, 8. Терм малое характеризуется нечеткой переменной малое, Х, C. Требуется построить функцию принадлежности нечеткого множества C, т. е. определить значение _С(х), хХ.

Пусть опросом экспертов получена следующая матрица парных сравнений:

Здесь, например, на пересечении первой строки и второго столбца стоит число 5, т. е. m₁₂=5, т. е. в следствие оценки эксперта _С(1) больше _С(3) в соответствии с таблицей.

Зафиксируем первый столбец матрицы М: М1 = 1, 1/5, 1/6, 1/7 и по формуле, приведенной выше найдем значения функций принадлежности в точках х_i, i = 1,2,3,4.

; ;

; .

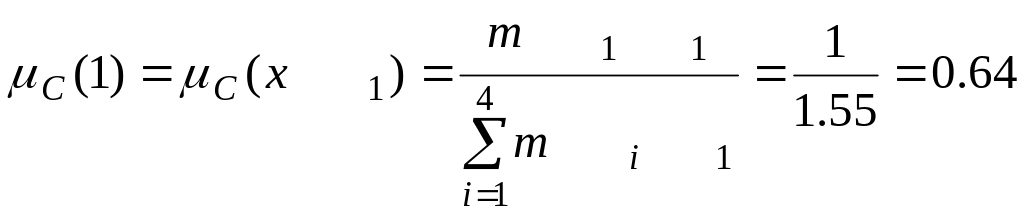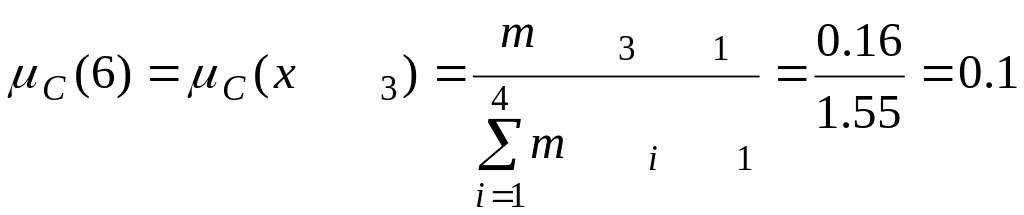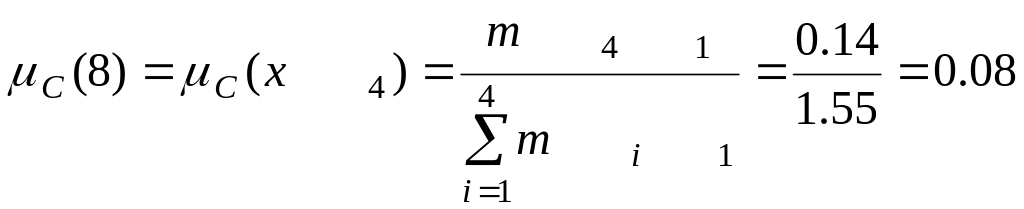Таким образом, нечеткое множество С имеет вид:

C = 0.64/1, 0.13/3, 0.1/6, 0.08/8.