1. Силы взаимодействия между молекулами жидкости относительно малы, поэтому поток жидкости, текущей в цилиндрической трубе можно представить в виде близко расположенных скользящих слоев.

Идеальная жидкость несжимаема и при движении молекул трение отсутствует. В реальной жидкости движение молекул приводит к возникновению силы трения. Сила, которая возникает между слоями текущей жидкости, и называется силой внутреннего трения или вязкостью.

В потоке движу­щейся жидкости выделим два соседних слоя, плошади которых S рас­пложены друг от друга на расстоянии Δх (рис. 3.1). Скорости этих слоев отличаются на малую величинуΔυ=υ1-υ2.

Между слоями возникает сила трения f, которая выражается формулой Ньютона:

3.1

Где градиент скорости

η –коэффициент динамической вязкости жидкости

S –площадь соприкосающихся слоев

η=f∙

Если s=1, то η численно равняется f, то есть коэффициент динамической вязкости численно равен силе внутреннего трения. Учитывая равномерность величин входящих в формулу 3.2, получим единицу измерения вязкости в СИ Н∙с/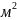 - Па∙с. В системе СГС коэффициент вязкости измеряется в Дин∙с/ - эта единица называется Пуазом (П). В медицинской практике используют единицу в 100 раз меньшую- сантипуаз (сП). Соотношение между единицами вязкости:

1 Н∙с/ = 10П; 1П= 100сП .

Когда слои жидкости текут параллельно, то течение жидкости называют ламинарным.

2. Изучая ламинарное течение через вертикально расположенные капилляры, Пуазейль установил, что объем жидкости, протекающей за промежуток времени t, выражается формулой:

,где Δp –разность давлений на концах капилляра

r – радиус капилляра

l – длина капилляра

η – коэффициент вязкости

Поскольку определение абсолютной вязкости является труд­ной задачей, то целесообразно использовать понятие относительной вязкости, которая равна отношению абсолютной вязкости исследуемой жидкости к вязкости эталонной жидкости (обычно это дистиллированная вода при 20 °С).

Метод определения относительной вязкости

Определение относительной вязкости жидкости производится вискозиметром Оствальда. Это стеклянный сосуд U-образной формы. Каждая трубка сосуда имеет расширение на разных высотах. Трубка с рас­ширением в верхней части имеет капилляр (рис. 3.2). Исследуемой жидкостью наполняется трубка, имеющая нижнее расширение. Жидкости должно быть столько, чтобы нижнее расширение было полностью заполнено. Затем при помощи резиновой груши жид­кость поднимается в трубку, имеющую верхнее расширение, выше метки т. Секундомером измеряется время t протекания жидкости от метки т до метки п. Это и будет время протекания жидкости через капилляр. После это­го вискозиметр хорошо промывают и просушивают. В дальнейшем таким же образом определяется время протекания такого же объема дистиллированной воды. Так как используется один и тот же вискозиметр и берутся одинаковые объемы, то:

3. Подтверждение закона Стокса демонстрационным экспериментом

Сила сопротивления при падении шарика радиусом г в жид­кости зависит от вязкости этой жидкости и определяется законом Стокса:

f = 6πηrv, (3.8)

где: υ - скорость равномерного движения шарика. Движение шарика бу­дет равномерным, если результирующая трех действующих на него сил (силы тяжести, Архимедовой силы и силы сопротивле­ния) будет равна нулю. Из условия равновесия следует:

6πηrυ= g(p-р'), (3.9)

где: р - плотность материала, из которого сделан шарик; - плотность жидкости

Из выражения (3.9) ясно, что:

η=

(3.10)

Исследуя одновременно падение двух шариков с разными ра­диусами г, и г, и учитывая, что u=S/t, получаем:

η=

(3.11)

и соответственно:

η=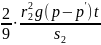

(3.12)

Приравнивая правые части выражений (3.11) и (3.12), получаем:

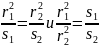
Из выражения (3.13) очевидно, что расстояния, пройденные шариками за одинаковый промежуток времени, отно­сятся как квадраты их радиусов.

Экспериментальное подтверждение выражения (3.13) косвенно подтверждает закон Стокса. Устройство, используемое для этой цели, представлено на рис. 3.3. Сосуд 1 наполнен вязкой жидкостью (например глицерином). Для проведения опыта катушка электромагнита питается от источника постоянного тока. При вра- щении устройства вокруг горизонтальной оси, шарики принимают исходное поло- жение. Радиусы шариков относятся как 1/2. При выключении тока одновременно начинают падать оба шарика.

Поскольку скорости шариков отно­сительно малы, зрительно констатирует­ся, что когда маленький шарик проходит отметку 2, отмеченную на шкале, находя-

щейся на стенке сосуда, большой шарик проходит отметку 8 (дальше, маленький шарик - отметку 3, большой - отметку 12). Расстояния, пройденные шариками за любые равные промежутки вре-мени, относятся как ¼. Результат эксперимента наглядно подтверждает выражение (3.13), а следовательно и закон Стокса.