1. Основные теоретические сведения

Все события делятся на детерминированные, случайные и неопределенные.

Если событие наступает в эксперименте всегда, оно называется достоверным, если никогда – невозможным. Это детерминированные события.

Статистическое определение вероятности: Если в опыте, повторяющемся n раз, событие появляется m_A раз, тогда относительная частота наступления события: . Р(А) – вероятность наступления события А.

Для достоверного события : Р()=1. Для невозможного события : Р()=0.

0  P(A)  1, т.к. 0m_An  0  hn(A)  1

 mA=n hn(A)=1

 m_A=0 hn(A)=0

Все мыслимые взаимоисключающие исходы опыта называются элементарными событиями. Наряду с ними можно наблюдать более сложные события – комбинации элементарных.

Несколько событий в данном опыте называются равновозможными, если появление одного из них не более возможно, чем другого.

2. Классическое определение вероятности: Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:

,

где m_A- число исходов, благоприятствующих появлению события А.

Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей.

1. Суммой (объединением) двух событий А и В называется новое событие А+В, заключающееся в проявлении хотя бы одного из этих событий.

2. Произведением (пересечением) двух событий А и В называется новое событие АВ, заключающееся в одновременном проявлении обоих событий. А*В=АВ, АА=А, АВА=АВ.

3. Событие А влечет за собой появление события В, если в результате наступления события А всякий раз наступает событие В. АÌВ

А=В: АÌВ, ВÌА

3. Теорема сложения вероятностей.

Вероятность суммы несовместных событий равна сумме вероятностей событий:

Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +…

Следствие. Если события A₁+A₂+…+A_n - полная группа событий, то сумма их вероятностей равна 1.

P(A+ ) = P(A) + P( ) = 1

Вероятность наступления двух совместных событий равна:

Р(А+В) = Р(А) + Р(В) - Р(АВ)

4. Теорема умножения вероятностей. Условные вероятности.

Опыт повторяется n раз, m_B раз наступает событие В, m_АВ раз наряду с событием В наступает событие А.

hn(B) = hn(AB) =

Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:

- условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.

5. Формула полной вероятности.

Вероятность события В, которое может произойти совместно только с одним из событий Н₁, Н₂, …Н_n , образующих полную группу событий, вычисляется по формуле:

События А₁, А₂, …А_n называют гипотезами.

6. Теорема гипотез (формула Байеса).

Если до опыта вероятности гипотез были Р(Н₁), Р(Н₂)…Р(Н_N), а в результате опыта произошло событие А, то условные вероятности гипотез находятся по формуле:

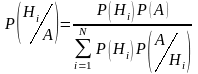
7. Повторение испытаний       Формула Бернулли 

где   - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

8. Общая теорема о повторении опытов

В отличие от частной теоремы она применяется когда вероятность появления каждого из событий не равны между собой

F(A₁)≠F(A₂) ≠F(A₃) ≠…

В этих случаях вероятности комбинаций приходится расписывать подробно. Так, вероятность появления одного любого из трех событий приходится вычислять по формуле:

При большом количестве n событий число комбинаций и, следовательно, число слагаемых существенно возрастает.

Для упрощения вычислений возможно применение производящей функции:

,

где p_i=F(A_i) – вероятность появления i-го события

q_i=1-F(A_i) – вероятность отсутствия i-го события

П - символ произведения

Для n=3 производящая функция равняется

При увеличении n количество сомножителей увеличивается. Результатом вычисления произведения является многочлен вида

j = a₀Z⁰+ a₁Z+ a₂Z²+ a₃Z³+ … + a_nZⁿ

где а₀, а₁, … а_n – коэффициенты при Z, представляющие числа из комбинаций q_i и p_i.

Каждый коэффициент численно равен вероятности появления такого количества событий, число которого равняется показателю степени Z. Так при отсутствии любого события показатель степени равняется 0, а вероятность равняется

При одновременном появлении всех n событий показатель степени равняется n, а вероятность равняется

Вероятность появления одного любого события из А₁, А₂, …, А_n будет равняться , а вероятность появления одновременно двух событий будет равняться F_n²=a₂ и т.д.

Применение производящей функции позволяет формализовать вычисление вероятностей появления событий и избежать применения более громоздкого математического аппарата теорем умножения и сложения