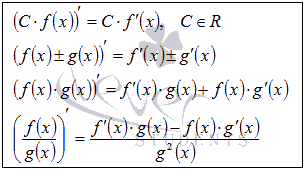1Ый и 2ой замечательный предел.
Первый замечательный предел
Второй замечательный предел
или 
Непрерывность функций и классификация. Теорема о непрерывн. Функции в точке. Теорема о непрерывн. Функциях в отрезках.
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Классификация точек разрыва:
- Устранимые точки разрыва
Если предел функции существует, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то
точка 
называется точкой
устранимого разрыва функции.
- Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Теорема
1.
Пусть
функция f (x) непрерывна
в точке x
= a, и C является
константой. Тогда функция Сf (x) также
непрерывна при x
= a.
Теорема
2.
Даны
две функции f (x) и g (x),
непрерывные в точке x
= a. Тогда
сумма этих функций f (x)
+ g (x) также
непрерывна в точке x
= a.
Теорема
3.
Предположим,
что две функции f (x) и g (x) непрерывны
в точке x
= a. Тогда
произведение этих функцийf (x) g (x) также
непрерывно в точке x
= a.
Теорема
4.
Даны
две функции f (x) и g (x),
непрерывные при x
= a. Тогда
отношение этих функций 
также
непрерывно при x
= a при
условии, что
.
Теорема
5.
Предположим,
что функция f (x) является
дифференцируемой в точке x
= a. Тогда
функция f (x) непрерывна
в этой точке (т.е. из дифференцируемости
следует непрерывность функции в точке;
обратное − неверно).
Теорема
6 (Теорема о предельном значении).
Если
функция f (x) непрерывна
на закрытом и ограниченном интервале [a,
b], то она
ограничена сверху и снизу на данном
интервале. Другими словами, существуют
числа m и M,
такие, что
Производная функции в точке. Дифференцируемость и непрерывность. Таблица производных. Правило дифференцирования.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке).
Непрерывность (см.18)
Основные правила дифференцирования
