10. Основные понятия аналитической геометрии. Векторная алгебра. Скалярное, векторное и смешанное произведение векторов.

Вектор - направленный отрезок на плоскости или в пространстве. Вектор свободен , относительно точки приложения, т.е. с сохранением длины и направления вектора.

Коллинеарные векторы расположены на одной или на параллельных прямых.

Скалярное произведение - это число, которое равно произведению длин на cos угла между векторами.

В ортонормированном базисе скалярное произведение векторов а и в равно сумме произведений одноимённых координат.

Ортогональность двух векторов проверяется с помощью скалярного произведения. Если скалярное произведение равно нулю, то один или второй, или оба ортогональны. С помощью скалярного произведения вычисляют работу силы.

Векторным произведением двух векторов называют 3 вектор d, который обладает тремя свойствами:

1)da, db

2)a,b,d

3)|d|=|a||b|sin(a,b)=S_{трапеции}

Свойства векторного произведения

1)[a,b]=-[b,a]

2)[a(b+c)]=[a,b]+[a,c]

3)[(a,b]=[a,b]

Если векторы ненулевые и коллинеарные, то [a,b]=0

Коллинеарность двух векторов проверяется с помощью векторного произведения.

Смешанное произведение 3-х векторов

abc=[a,b]c=dc

Заметим, что с геометрической точки зрения смешанное произведение векторов, такое, которое интерпритируют как +V параллелепипеда, если тройка правая, -V, если левая.

Если угол острый, abc=+V, если тупой abc=-V

Если 3 вектора, отличные от нуля, компланарны, то V=0, abc=0

11. Плоскость в пространстве.

Всякое уравнение первой степени вида ax+by+cz+d=0, в пространстве задаёт плоскость, и обратно, всякая плоскость задаётся уравнением этого вида.

Пусть A0, x₀=(-b/a)y₀-(c/a)z₀-d

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

Уравнение геометрически задаёт в пространстве плоскость, которая проходит через N₀ и проходит через М. Чтобы вывести уравнение геометрического места точек надо на этом геометрическом месте взять текущую точку, считать её известной, связать координаты текущей точки с помощью условия.

Нормальное уравнение плоскости отличается: все коэффициенты не превышают единицы, свободный член отрицателен, сумма квадратов коэффициентов равна 1.

С помощью нормального уравнения можно определить расстояние от точки до плоскости.

Расстояние равняется модулю отклонения. (()M^*)=d>0; d=||

=+d, если угол острый, M^*, 0 по разные стороны, -d, если угол тупой M^*, 0 в одну сторону.

12. Прямая линия в пространстве и на плоскости.

Задаётся двумя плоскостями, которые пересекаются по этой прямой. Прямую можно задать точкой и направляющим вектором.

x-x₀/e=y-y₀/m=z-z₀/p – канонические вектора.

Всякая прямая линия на плоскости задаётся уравнением 1 степени вида: Ax+By+C=0 и обратно.

Чтобы привести общее уравнение к нормальному, надо найти нормирующий вектор =1/sqrt(A²+B²)

13. Эллипс, гипербола и параболы.

Эллипс- Это геометрическое место точек плоскости, сумма расстояний которых до двух фиксированных точек F1, F2, называемая фокусами есть величина постоянная равная 2а(а>0) и при этом 2а>2c(c>0)- расстояние между фокусами.

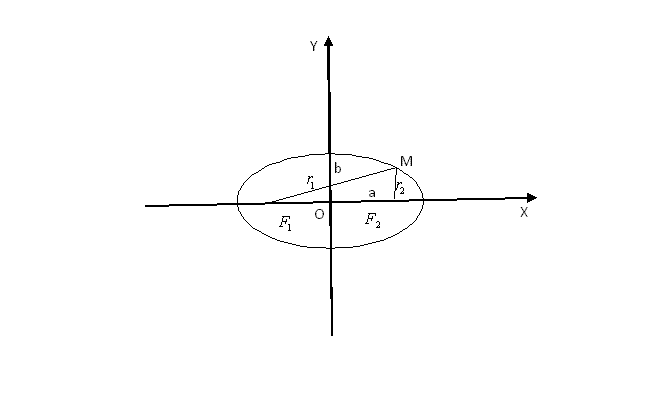
r1+r2=2a F1(-C;0), F2(C;0)

sqrt((x+c)²+y²)+sqrt((x-c)²+y²)=2a

x²/a²+y²/b²=1 b²=a²-c²

Свойства:

Эллипс имеет полную симметрию.

y²/b²=1- x²/a²

Оптическое свойство эллипса.

Точки на оси A₁(-a;0) A₂(a;0)- вершины

2а- большая ось.

B₁(0;b), B₂(0;-b)

2b-малая ось

x=acost y=bsint

Вводится понятие эксцентриситет- это число Е=с/a, c<a , E<1

E=sqrt(a²-b²)/a=sqrt(1-(b/a)²), b<<a, тогда Е1

Если b=a, Е0.

Для характеристики эллипса вводят понятие директрисса. Две прямые расположены вне эллипса.

Е<1, |x|>a r/d=E

Гипербола- геометрическое место точек плоскости, разность расстояний которых до двух фиксированных точек, называемых фокусами, величина постоянная, равная +-2a, F1,F2- фокусы, и при этом 2а<2c< c>0< 2c- расстояние между фокусами.

r1-r2=+-2a

sqrt((x+c)²+y²)-sqrt((x-c)²+y²)=+-2a

x²/a²-y²/b²=1

c²=a²+b²

E=c/a>1 x=+-a/E

Парабола

y²=2p_x

Эллипс, гипербола и парабола являются сечениями конуса.