4. Миноры матрицы. Ранг матрицы. Элементарные преобразования матрицы.

Нахождение минора.

Например, есть матрица:

Предположим, надо найти дополнительный минор  . Этот минор — определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:

   

Получаем 

Рангом системы строк (столбцов) матрицы   с   строк и   столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

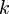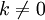• прибавление к любой строке матрицы другой строки.

5. Арифметическое пространство строк. Линейная зависимость. Свойство линейной зависимости. Теорема о базисном миноре.

Арифметическое пространство – это пространство строк и столбцов с элементами из множества вещественных чисел.

- пространство столбцов длины n.

- пространство столбцов длины n.

- пространство строк длины n

В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.

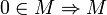•  линейно зависимо

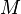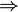
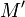•  линейно независимо     линейно независимо для всех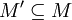 

•  линейно зависимо     линейно зависимо для всех 

Теорема о базисном миноре

Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.

6. Теорема о совместности. Произвольные слау.

Определение 1. Решением системы называется такая совокупность n чисел  ,  ,...,  , что при подстановке их во все уравнения системы вместо соответствующих неизвестных получаются числовые тождества. Определение 2. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения - несовместной. Определение 3. Система, имеющая единственное решение, называется определенной; система, имеющая более одного решения - неопределенной. Определение 4. Две системы называются эквивалентными, если множества их решений совпадают. Определение 5. Матрица  получаемая из матрицы А системы добавлением столбца свободных членов, называется расширенной матрицей.

Теорема о совместности.

Система АХ=В совместна тогда и только тогда, когда ранг матрицы равен рангу расширенной , полученной из основной путём приписывания свободных членов.