42.Объяснить на примере что такое сложный процент, какие есть его функции? Объяснить термины: будущая и настоящая стоимость единицы и аннуитета?

Аннуитет— это серия равновеликих платежей, первый из которых осуществляется через один период, начиная с настоящего момента, т.е. платеж производится в конце рассматриваемых периодов. Сложные проценты – это особый вид начисления процентов в банковском депозите, при котором по окончании каждого периода начисленные проценты становятся основной суммой. Таким образом, в следующем периоде проценты начисляются на большую сумму, чем в предыдущем, за счет чего вклад растет со скоростью экспоненты. Учеными разработаны специальные таблицы шести функций денежной единицы, помогающие экспертам-оценщикам вести расчеты с использованием сложных процентов. Таблицы состоят из шести граф (колонок), в которых помещены значения, полученные исходя из шести функций денежной единицы.

1. Будущая стоимость единицы. Эта функция, определяющая величину будущей стоимости сегодняшней денежной единицы через «n» периодов при сложном проценте равном «i»:

Sn=(1+i)n где Sn – накопленная сумма после периода «n»; i – величина сложного процента; n – количество периодов.

2. Настоящая стоимость единицы – величина, обратная будущей стоимости. Данная функция соответствует сегодняшней стоимости одной денежной единицы, полученной через «n» периодов при «i» процентах годовых:

3. Настоящая стоимость обычного единичного аннуитета. Функция определяет настоящую стоимость серии будущих равных единичных платежей в течении «n» периодов при «i» процентах годовых. Использует коэффициент аннуитета или коэффициент Инвуда, определяемый как сумма коэффициентов настоящей стоимости единицы за «n» периодов при «i» процентах годовых:

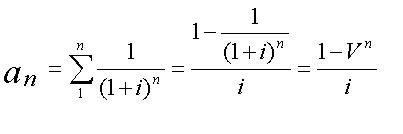
4. Взнос на амортизацию единицы. Определяет какой должен быть размер платежей в течение «n» периодов, чтобы их настоящая стоимость при норме процентов «i» была равна единице. Функция применяется при расчете платежей по погашению кредита, если эти платежи предполагаются одинаковыми по величине, при этом каждый платеж включает и выплату процента и погашение по основной сумме кредита. Настоящую стоимость кредита можно рассчитать как сумму, превращающуюся в серию платежей величиной:

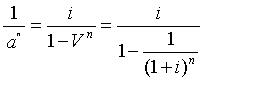
5. Будущая стоимость аннуитета. Показывает какую будущую сумму даст единичный аннуитет при заданном числе периодов и норме процента. Практика депонирования одинаковых платежей и накопления их до определенной суммы широко распространена и называется формированием фонда возмещения. Величины коэффициентов будущей стоимости аннуитета рассчитываются по формуле:

С другой стороны, накопление единицы за период соответствует будущей стоимости величины настоящей стоимости единичного аннуитета в конце периода «n» и определяется по формуле:

6. Коэффициент фонда возмещения. Определяет величину платежа аннуитета, будущая стоимость которого через «n» периодов при заданной сумме процентов равна единице. Этот коэффициент дисконтирует будущую стоимость единичного фонда возмещения в серию равновеликих платежей. Применяется данная функция при расчете депонируемых платежей, которые должны сформировать к определенному моменту в будущем требуемый остаток на счете. Коэффициент фонда возмещения является обратныой величиной коэффициента будущей стоимости аннуитета.