11. Основные виды простых суждений

Суждения бывают простые и сложные. Простое суждение - это суждение, в котором есть только один субъект и один предикат.

Например, «Некоторые преступления являются неумышленными». В логической форме: «Нек. S есть Р».

Сложное суждение - это суждение, имеющее в своем составе более одного субъекта или предиката. Его можно рассматривать как суждение, состоящее из нескольких простых суждений.

Например. суждение «Права авторов, рационализаторов и изобретателей охраняются государством» состоит из трех простых суждений: «Права авторов охраняются государством», «Права рационализаторов охраняются государством» и «Права изобретателей охраняются государством». Их можно обозначить любыми маленькими буквами латинского алфавита: а, Ь, с, каждая из которых представляет простое суждение как нерасчлененное целое, (логическая структура простого суждения не раскрывается).

Виды простых суждений:

1) По характеру предиката различают.

а) суждения атрибутивные ( от лат. - «свойство», «признак») или суждения о свойствах - это суждения, в которых отражается связь между предметом и его свойствами. Эта связь утверждается или отрицается. Например, «Некоторые люди любят путешествовать» или «Некоторые люди не любят путешествовать». Логическая форма атрибутивных суждений:

«Нек (все) S есть Р» или «Нек. (все) S не есть Р».

Простые атрибутивные суждения называются также категорическими ( от греч. - «ясный», «безусловный», «не допускающий иных толкований»),

б) суждения релятивные (от лат. «отношение») или суждения об отношениях - это суждения, отражающие в качестве характеристики предмета его отношения с другими предметами.

Например, «Мораль возникла раньше права».

Отношения, которые отражаются в релятивных суждениях, могут быть разного характера: отношения равенства, временные отношения, пространственные отношения, причинно-следственные отношения.

Суждения об отношениях имеют логическую структуру, отличающуюся от структуры атрибутивных суждений. Поэтому они могут быть представлены специальной формулой: х R у, где хну- члены отношения (в вышеприведенном случае - «мораль» и «право»), a if - отношение между ними.

Однако, релятивные суждения могут быть преобразованы в атрибутивные и записаны в классической форме суждения «S есть (не есть) Р».

При этом отношение между предметами интерпретируется как признак одного и них (признак субъекта): «Мораль (S) есть то, что возникло раньше права (Р)».

в) суждения экзистенциальные (от лат. - «существование») или суждения о существовании - это суждения, в которых раскрывается сам факт существования или несуществования предмета.

Например, «Существуют исключения из правил».

Суждения о существовании обладают определенной спецификой, но и их целесообразно рассматривать как частный случай атрибутивных суждений. Предикатом суждения в этом случае выступает понятие о существовании или несуществовании предмета.

Например, «Исключения из правил (S) есть то, что существует (Р)».

2. По качеству (по характеру связки) различают:

а) утвердительные суждения - это суждения, выражающие принадлежность предмету некоторого признака.

Например. «Религия (S) есть ненаучное мировоззрение (Р) ». Логическая форма суждения: « Все S есть Р ».

б) отрицательные суждения - это суждения, выражающие отсутствие признака у предмета.

Например. « Религия (S) не является наукой (Р) ». Логическая форма суждения: «Все S не есть Р».

2. По количеству суждения различают:

а) единичные суждения - это суждения, в которых нечто высказывается об отдельном предмете, то есть субъектом в этих суждениях выступают единичные понятия.

Например, «Москва (S) - столица России (Р) ». Логическая форма суждения: « S есть Р ».

б) частные суждения - это суждения, в которых что- либо утверждается о части какой-то группы предметов. В русском языке они выражаются такими словами, как «некоторые», «не все», «многие», «большинство» и т.д.

Например. «Большинство студентов нашей группы (S) хорошо сдали экзаменационную сессию (Р) » или «Многие люди (S) не обладают абсолютным слухом (Р)».

Логическая форма этих суждений: «Некоторые S есть Р» и «Некоторые S не есть Р».Иногда, кванторное слово, вообще может отсутствовать, но по смыслу суждение носит именно частный характер.

Например. «Людям (S) свойственно ошибаться (Р)». Здесь не утверждается, что свойство ошибаться относится к каждому человеку и всегда проявляется. Понятие «люди» взято в собирательном смысле. Поэтому суждение носит частный характер и его логическая форма «Некоторые S есть Р».

в) общие суждения - это суждения, в которых что- либо утверждается обо всем классе предметов и притом в разделительном смысле (указанные признаки принадлежат каждому элементу класса). В русском языке такие суждения выражаются словами «все», «всякий», «каждый», «любой» и т.д. (в утвердительных случаях) или «ни один», «никто», «никакой» и т.д. (в отрицательных случаях).

Например, «Каждый человек (S) имеет свой характер (Р) » или «Ни один закон (S) не противоречит морали (Р) ». Логическая форма этих суждений: «Все S есть Р» и «Ни одно S не есть Р».

Иногда в языковом выражении кванторное слово может вообще отсутствовать, но по смыслу утверждение носит общий характер и суждение является общим.

Например, «Равнодушие унижает», «Сделка, не соответствующая требованиям закона, не признается действительной» и т.д. В этих суждениях по смыслу предикат относится к каждому элементу класса: «Всякое равнодушие...», «Ни одна сделка...», и логическая форма этих суждений: «Все S есть Р» и «Ни одно S не есть Р».

Особое место в классификации суждений по количеству занимают уточняющие суждения выделяющие и исключающие. Выделяющие суждения отражают тот факт, что признак, выраженный предикатом, принадлежит только данному предмету (предметам).

Например, «Только Иванов написал контрольную работу на отлично» или « Только некоторые студенты нашей группы изучают французский язык». Логическая форма этих суждений: «Только это S есть Р» и «Только некоторые S есть Р».

Выделяющие суждения могут быть единичными («Только студент Иванов бывал в Риме на экскурсии»), частными («Некоторые преступники - рецидивисты») и общими («Уголовное наказание применяется только по приговору суда»). Выделяющие суждения выражаются предложениями со словами «только», «лить», и т.д., которые могут стоять как перед субъектом, так и перед предикатом, но могут и вообще отсутствовать. В этих случаях установить, что данное суждение является выделяющим, помогает логический анализ.

Исключающие суждения - это суждения, в которых утверждается принадлежность (или непринадлежность) признака всем предметам, за исключением некоторой части.

Например, «Все студенты, кроме Иванова, написали контрольную работу хорошо». Логическая форма этого суждения: «Все S, кроме S*, есть Р».

Исключающие суждения выражаются

предложениями со словами «кроме», «за исключением», «помимо», «не считая» и т.д. Значение выделяющих и исключающих суждений состоит в том, что положения, выраженные в форме этих суждений, характеризуются особой точностью и определенностью. Именно поэтому ряд научных положений и статей международных документов, законов государства выражен в форме выделяющих или исключающих суждений.

Например, в Конституции Российской Федерации указывается: «Правосудие в Российской Федерации осуществляется только судом».

4) Объединенная классификация суждений по количеству и качеству.

Так как все суждения имеют количественную и качественную характеристику, то чаще всего используют объединенную классификацию суждений, где выделяют четыре основных вида суждений:

1. общеутвердительные суждения (вид А - первая гласная буква от лат. affirmo - «утверждаю») - по количеству общие, а по качеству утвердительные: «Все S есть Р».

2. частноутвердительные суждения (вид I - вторая гласная буква того же слова) - по количеству частное, а по качеству утвердительное:

«Нек. S есть Р».

3. общеотрицательные суждения (вид Е - первая гласная буква от лат. nego -«отрицаю») - по количеству общее, а по качеству отрицательное: «Ни одно S не есть Р».

4. частноотрицательные суждения (вид О - вторая гласная буква того же слова) - по количеству частное, а по качеству отрицательное:

«Нек. S не есть Р».

Чтобы правильно понимать смысл суждений и правильно оперировать ими, необходимо знать распределенность терминов в суждениях - субъекта и предиката. Термин считается распределенным, если в суждении он мыслится в полном объеме, а нераспределенным - если он мыслится не во всем объеме, а частично. Общее правило: субъект всегда распределен в общих суждениях (А и Е), а предикат - в отрицательных суждениях (I и О). Из этого общего правила есть исключение, касающееся выделяющих суждений:

1. если общеутвердительное суждение является выделяющим, то субъект и предикат имеют одинаковый объем, и распределены будут и субъект, и предикат. Например, «Все квадраты (и только квадраты) являются прямоугольными ромбами».

2. Если частноутвердительное суждение является выделяющим, то предикат полностью входит в объем субъекта, и субъект будет не распределен, а предикат распределен.

Например, в суждении «Некоторые родители (и только некоторые) являются многодетными» понятие «многодетные» (Р) полностью входит в объем понятий «родители» (S).

Проверить распределенность терминов в суждениях всегда можно с помощью кругов Эйлера, изобразив соотношение объемов понятий, которые являются субъектом и предикатом в суждении.

Сводная таблица распределенности терминов приведена на (рис. 11).

Таблица распределенности терминов в суждениях

Термины в суждении	А	Е	I	О
S	+	+	-	-
Р	-	+	-	+
Р	+	+	+	+
выделяющих суждений

Рис. 11

12. Логические отношения между простыми суждениями

Логические отношения между суждениями устанавливаются с точки зрения их сходства по смыслу и возможности быть одновременно истинными. В силу этого логические отношения устанавливаются лишь между сравнимыми суждениями.

Сравнимыми называются суждения, у которых одинаковые субъекты и предикаты, но различные количетвенно-качественные характеристики.

Например, сравнимыми являются суждения: «Все металлы (S) электропроводны (Р) » и «Некоторые металлы (S) не являются электропроводными (Р)».

Логические отношения между простыми сравнимыми суждениями обычно наглядно представляют с помощью схемы, называемой логический квадрат (рис.12)Его вершины обозначают основные типы простых категорических суждений - А, I, Е, О; стороны и диагонали квадрата - логические отношения между суждениями.

Между сравнимыми простыми суждениями существует два вида логических отношений: совместимости и несовместимости.

Отношения совместимости - это отношения между суждениями, которые могут быть одновременно истинными, так как они выражают одну и ту же мысль полностью или хотя бы частично.

Различают три вида совместимости: 1)

Рис. 12

эквивалентность (полная совместимость); 2) частичная совместимость (субконтрарностъ); 3) подчинение.

1. Эквивалентность - это логическое отношение между такими суждениями, которые имеют одинаковые субъекты и предикаты, однотипную - утвердительную или отрицательную - связку, одну и ту же выраженную квантором количественную характеристику. Эквивалентные (равнозначные) суждения выражают одну и ту же мысль в различной языковой форме: субъект и предикат могут быть выражены словами-синонимами или на разных языках. Например, «Это - стол» и «It is a table».

Эквивалентные суждения всегда одновременно истинны или ложны (полная совместимость). С помощью логического квадрата отношение эквивалентности не иллюстрируется.

2. Частичная совместимость (субконтрарность) -

это отношение между двумя частными суждениями разного качества, то есть между суждениями частноутвердительным (I) и частноотрицательным (О). Их логические формы:

«Нек. S есть Р» и «Нек. S не есть Р».

Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. При ложности одного из них другое будет обязательно истинным. При истинности одного из них - другое может быть как истинным, так и ложным. В логическом квадрате отношение частичной совместимости (субконтрарности) представлено нижней горизонталью.

3. Подчинение - это логическое отношение между суждениями одного качества, но разного количества, то есть: между суждениями общеутвердительным (А) и частноутвердительным (I), а также между суждениями общеотрицательным (Е) и частноотрицательным (О).

Таким образом, в отношении подчинения находятся: 1) «Все S есть Р» и «Нек S есть /*»;

2) «Ни одно S не есть Р» и «Нек. S не есть Р».

Для отношения подчинения характерны две зависимости. Во-первых, при истинности общего суждения частное суждение всегда будет истинным. Во- вторых, при ложности частного суждения общее суждение также будет ложным. В логическом квадрате отношения подчинения представлены вертикальными сторонами квадрата (слева - утвердительные суждения; справа - отрицательные суждения).

Отношения несовместимости это отношения между суждениями, которые не могут быть одновременно истинными.

Существует два вида отношений несовместимости: 1) противоположность (контрарность) и 2) противоречие (контрадикторность).

1. Противоположность (контрарность) - это

отношение между двумя общими суждениями разного качества, то есть между общеутвердительным (А) и общеотрицательным (Е) суждениями. Их логическая форма:

«Все S есть Р» и «Все S не есть Р».

Эти суждения не могут быть одновременно истинными, но могут быть одновременно ложными. При истинности одного из них другое обязательно будет ложным. При ложности одного - другое может быть как истинным, так и ложным. В логическом квадрате отношение противоположности (контрарности) представлено верхней горизонталью.

2. Противоречие (контрадикторность) - это

отношение между суждениями разного качества и разного количества, которые не могут быть одновременно ни истинными, ни ложными, но всегда имеют различное значение истинности. Таким образом, это отношение между суждением (А) общеутвердительным и суждением (О) частноотрицательным, а также между суждением (Е) общеотрииател ьным и суждением (I)

частноутвердител ъны.

При истинности суждения (А) - суждение (О) обязательно ложно, и наоборот. Можно сказать, что это отношение полной несовместимости. В логическом квадрате отношения противоречия (контрадикторности) представлены диагоналями квадрата.

Соответственно отношениям, в которых суждения находятся, квалифицируются и называются сами суждения: эквивалентные, подчиняющие и подчиненные, субконтрарные, противоположные (контрарные) и противоречащие (контрадикторные).

Например, для суждения «Все люди обладают сознанием», чья логическая форма «Все S есть Р» (А), противоречащим суждением будет «Некоторые люди не обладают сознанием», чья логическая форма «Нек. S не есть Р» (О), так как между ними логическое отношение противоречия (контрадикторности).

14. Логические операции с простыми суждениями

Логическими операциями с простыми суждениями называются простейшие их преобразования с целью уточнения информации, в них содержащейся. К ним относятся: превращение, обращение, противопоставление предикату и противопоставление субъекту.

1. Превращение (обверсия) - логическая операция, в ходе которой изменяется качество исходного суждения и заменяется предикат на понятие, противоречащее ему. Превращение опирается на правило: двойное отрицание равносильно утверждению. Двойное отрицание вводится путем замены связки на противоположную («есть» на «не есть» и наоборот) и замены предиката (Р) на его отрицание (не-Р). Количественная характеристика суждения при этом не меняется.

Например, суждение «Все адвокаты(З) - юристы (Р)» имеет логическую форму «Все S есть Р». В результате операции превращения мы получает: «Все S не есть не-Р», то есть в языковом выражении: «Все адвокаты не являются не юристами». Правильность проведенной операции можно проверить с помощью кругов Эйлера. Схема, изображающая отношение объемов S и Р в исходном суждении, должна соответствовать и результату логического преобразования. Все логические операции не изменяют информацию, но только уточняют ее.

2. Обращение (конверсия) - логическая операция, в ходе которой субъект и предикат меняются местами, при этом качество суждения не меняется.

Например, суждение «Некоторые растения (S) являются лекарственными (Р)» имеет логическую форму «Нек. S есть Р». В результате операции обращения мы получает: «Нек. Ресть S», то есть в языковом выражении: «Некоторое являющееся лекарственным (нечто обладающее лекарственным эффектом) есть растение».

Количественная характеристика суждения в ходе операции обращения может меняться. Поэтому надо знать правила операции обращения:

а) без изменения количества, обращаются суждения, где оба термина распределены или оба термина не распределены.

Например, суждение (Е) «Ни одно S не есть Р» обращается в суждение (Е) «Ни одно Р не есть S»; также суждение (I) «Нек. S есть Р» обращается в суждение в (I) «Нек. Р есть S».

б) в суждении (А), где субъект распределен, а предикат нераспределен, в результате операции обращения меняется количественная характеристика с общей на частную (обращение с ограничением).

Например. суждение «Все S есть Р» обращается в суждение «Нек. Р есть S».

в) суждение частноотрицательное (О) не обращается.

Из вышеприведенных правил исключения составляют выделяющие суждения:

суждение общеутвердительное (А) выделяющее обращается в суждение общеутвердительное (А). - суждение частноутвердительное (I) выделяющее обращается в суждение общеутвердительное (А).

Например, суждение «Только некоторые города (S) - столицы государств (Р)» имеет логическую форму «Только нек S есть Р» обращается в суждение «Все Р есть S» - « Все столицы государств есть города».

3. Противопоставление предикату - это

логическая операция преобразования суждения, в результате которого субъектом становится понятие, противоречащее предикату исходного суждения (не-Р), а предикатом - субъект исходного суждения (S). Противопоставление предикату можно рассматривать как результат последовательного проведения операций превращения и обращения. Проводится в два этапа:

1. проводится операция превращения исходного суждения, устанавливая отношение S к не-Р,

2. суждение, полученное путем превращения, обращается, в результате чего устанавливается отношение не-Р к S.

Количественные и качественные характеристики суждения в процессе операции противопоставления предикату могут меняться согласно правилам операций превращения и обращения.

Например. суждение «Все люди(8) смертны (Р) » имеет логическую форму «Все S есть Р».

В процессе противопоставления предикату это суждение преобразуется; 1) «Ни одно S не есть не-Р» 2) «Ни одно не-Р не есть S», что в языковом выражении означает: «Ни один бессмертный не есть человек».

4. Противопоставление субъекту - логическая операция преобразования суждения, в результате которого субъектом становится предикат исходного суждения (Р), а предикатом - понятие, противоречащее субъекту исходного суждения (не-S).

Противопоставление субъекту также можно рассматривать как результат последовательного проведения операций обращения и превращения. Проводится в два этапа:

1. сначала проводится операция обращения исходного суждения, устанавливающая отношение Р к S;

2. потом суждение, полученное путем обращения, превращается, в результате чего устанавливается отношение Р к не-S.

Количественные и качественные характеристики суждения в процессе операции противопоставления субъекту также могут меняться согласно правилам обращения и превращения.

Например, то же самое суждение «Все люди (S) смертны (Р)» с логической формой «Все S есть Р», в процессе противопоставления субъекту преобразуется: 1) «Нек. Р есть S» 2) «Нек. Р не есть не-S». В языковом выражении: «Некоторые смертные не есть не - люди».

15. Виды сложных суждений и условия их истинности

Сложным называют суждение, состоящее из нескольких простых, связанных логическими связками. Вид сложного суждения определяется характером логической связки. Соответственно выделяют следующие основные виды сложных суждений:

1. Конъюнктивными (соединительными) называются суждения, состоящие из нескольких простых, связанных логической связкой «конъюнкция» - а - (в русском языке ей соответствует соединительный союз «и»).

Например, «По реке плыли корабли (а), лодки (Ь) и другие предметы (с)». В состав данного суждения входит три простых суждения: (а) «По реке плыли корабли»; (Ь) «По реке плыли лодки»; (с) «По реке плыли другие предметы». Символическая запись: а, Ь, с.

Конъюнктивное сложное суждение истинно при истинности всех составляющих его простых суждений и ложно при ложности хотя бы одного из них. Условия истинности такого суждения наглядно показаны в сводной таблице на (рис. 13), где истинность суждения обозначена - и, а ложность - л. В-первых двух столбцах таблицы а и Ь, обозначающие простые суждения, берутся как независимые, и потому учитываются все возможные сочетания их значений истинности: ии, ил, ли, лл. В третьем столбце показано значение сложного конъюнктивного суждения. Из четырех построчных вариантов истинным оно является лишь в 1-й строке, когда истинны оба простых суждения: а и Ь.

Условия истинности простых суждений

а	Ь	а л b	a v b	a v b	а -» b	as Ь
и	и	и	и	л	и	и
и	л	л	и	и	л	л
л	и	л	и	и	и	л
л	л	л	л	л	и	и

Рис. 13

Во всех остальных случаях оно ложно либо в силу ложности одного из членов конъюнкции, либо в силу ложности обоих членов конъюнкции.

2. Дизъюнктивными (разделительными)

называются суждения, состоящие из нескольких простых суждений, связанных логической связкой «дизъюнкция» - v - (в русском языке ей соответствует разделительный союз «или»). Дизъюнкция бывает двух типов - нестрогая (слабая) дизъюнкция и строгая (сильная) дизъюнкция. Соответственно различают:

а) суждения нестрогой (слабой) дизъюнкции,

в которой связка употребляется в соединительно- разделительном значении.

Например, «Экскурсии бывают автобусные и пешеходные». Связка «или» в данном случае разделяет два возможных вида экскурсии, но возможно и их соединение. Условия истинности суждений нестрогой (слабой) дизъюнкции представлены в четвертом столбце таблицы (рис. 13): суждение будет истинным при истинности хотя бы одного члена дизъюнкции (1,2,3-я строки - ии, ил, ли) и суждение будет ложным при ложности всех ее членов (4- я строка -лл).

б) суждения строгой (сильной) дизъюнкции, в

которой связка «или» употребляется в строго разделительном значении: «либо - либо».

Например, «Данная экскурсия может состояться только либо во вторник, либо в четверг». Члены строгой дизъюнкции, называемые альтернативами, не могут быть одновременно истинными. Условия истинности суждений строгой (сильной) дизъюнкции представлены в пятом столбце таблицы (рис. 13): суждение будет истинным при истинности одного и ложности другого члена дизъюнкции (2, 3-я строки - ил, ли) и суждение будет ложным, если оба члена строгой (сильной) дизъюнкции (1-я строка - им) или оба ложны (4-я строка - лл).

3. Импликативными (условными) называются суждения, состоящие из двух простых суждений, связанных логической связкой «импликация» —* (в русском языке ей соответствует условный союз «если..., то...»).

Например, «Если предохранитель плавится, то электролампа гаснет».

В форме импликативных суждений могут быть представлены разные виды объективных связей: причинно- следственные, функциональные, временные, правовые, семантические и т.д. Приведенный выше пример раскрывает причинно-следственную связь. Именно на этом примере легче всего запомнить условия истинности этого вида сложных суждений.

В целом условия истинности импликативных (условных) суждений показаны в шестом столбце таблицы (рис. 13): суждение будет истинным во всех случаях, кроме одного - при истинности предшествующего и ложности последующего простого суждения (2-я строка - ил) импликация будет ложной. Применительно к вышеприведенному примеру суждение ложно, когда «есть причина» и «нет следствия».

3. Эквивалентными (двойная импликация)

называются суждения, включающие в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью.

Символ связки эквиваленции = или ( в русском языке ей соответствует сложный союз «если и только если..., то...»).

Например. «Если и только если человек достиг пенсионного возраста, то он имеет право на пенсию по старости». Логическая характеристика этого суждения состоит в том, что истинность предшествующего суждения (а) - «Если и только если человек достиг пенсионного возраста» - рассматривается как необходимое и достаточное условие истинности последующего утверждения (Ь) - «он имеет право на пенсию по старости». Точно так же истинность последующего утверждения b является необходимым и достаточным условием истинности предшествующего утверждения а.

Условия истинности эквивалентного суждения (суждения двойной импликации) представлены в седьмом (последнем) столбце таблицы (рис.13), эквивалентное суждение истинно в тех случаях, когда оба суждения принимают одинаковые значения, являясь одновременно либо истинными (1-я строка - мм), либо ложными (4-я строка - лл). Во всех остальных случаях, когда значения простых суждений не совпадают, эквивалентное суждение будет ложным (2,3-я строки - мл, ли).

Сложные суждения - конъюнктивные, дизъюнктивные (строгой и нестрогой дизъюнкции), импликативные и эквивалентные - используются в обычных рассуждениях деловых документах как самостоятельно, так и в различных сочетаниях.

Так, например, «Если мы поедем в Санкт-Петербург, то обязательно посетим Эрмитаж и Русский музей». Это комбинированное сложное суждение можно разбить на три простых:

1) «Если мы поедем в Санкт-Петербург» (а); 2) «мы обязательно посетим Эрмитаж» (Ь); 3) «мы обязательно посетим Русский музей» (с).

В целом это импликативное суждение, где предшествующим суждением выступает суждение 1 (а), а последующим - сложное суждение, состоящее из суждений 2 (Ь) и 3 (с), соединенных логической связкой конъюнкция. Условия истинности таких комбинированных сложных суждений определяются по таблице, где первый, второй и третий столбец показывают значение истинности и ложности простых суждений а,Ь,с; четвертый столбец показывает нам значение конъюнктивного сложного суждения (конъюнкция связывает суждения b и с), выступающего в качестве последующего суждения в импликативном сложном суждении; пятый столбец показывает окончательное значение импликативного суждения.

При наличии трех переменных (трех простых суждений, значение которых может быть различным) значение их истинности (и) и ложности (л) задаются в таблице следующим образом: 1-я строка - все и (иии); 2, 3, 4-я строки - две и и одна л (иил, или, лии), 5, 6, 7-я строки - одна и и две л (илл, лил, лли), 8-я строка - все л (ллл). Таким образом, таблица показьюает все возможности сочетания значений переменных (простых суждений, входящих в состав сложного комбинированного суждения). Истинным наше вышеприведенное суждение будет во всех случаях, кроме трех - 2 (мил), 3 (или) и 5 (илл) - (рис. 14).

Сложные суждения, как и простые суждения, могут находиться в разных отношениях. В частности отношение эквивалентности позволяет выражать одни сложные суждения через другие, что может иметь важное практическое значение при логическом анализе документов.

К таким широко известным и часто используемым эквивалентностям относятся законы де Моргана:

1. Выражение конъюнкции через дизъюнкцию - первый закон де Моргана гласит: «Отрицание конъюнкции тождественно дизъюнкции отрицаний». Записать это можно в виде символического выражения:

l(aAB)slavlB

2. Выражение дизъюнкции через конъюнкцию - второй закон де Моргана гласит: «Отрицание дизъюнкции тождественно конъюнкции отрицаний». Записать это можно в виде выражения:

1(аvB)slaA]e

Законы де Моргана оказываются чрезвычайно полезными при уточнении информации, содержащейся в документах.

Таблица истинности и ложности сложных суждений

а	Ь	с	b А с	а —> (Ь л с)
и	и	и	и	и
и	и	л	л	л
и	л	и	л	л
л	и	и	и	и
и	л	л	л	л
л	и	л	л	и
л	л	и	л	и
л	л	л	л	и

Рис. 14

16. Умозаключение как форма мышления

Третьей формой мышления является умозаключение. Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение.

Специфика умозаключения состоит в том, что с его помощью из уже имеющегося знания, выраженного в тех или иных суждениях, мы можем получить новое знание, не обращаясь при этом непосредственно к опыту, к действительности.

Любое умозаключение состоит из посылок, заключения и вывода. Посылками умозаключения называют исходные суждения, из которых выводится новое суждение. Заключением называется новое суждение, полученное логическим путем из посылок. Логический переход от посылок к заключению называется выводом.

Например, «Все люди смертны (1). Сократ - человек (2). Следовательно, Сократ смертен (3)». В этом умозаключении 1-е и 2-е суждения являются посылками, 3-е суждение - заключением.

При логическом анализе умозаключения посылки и заключение принято записывать в столбик, располагая их отдельно, друг под другом. Заключение записывают под горизонтальной чертой, отделяющей его от посылок и обозначающей логическое следование.

Слова «следовательно», «значит», «поэтому» и близкие им по смыслу, с помощью которых формулируют логический вывод, под чертой уже не пишут. Выражение «подвести черту» и означает сделать вывод. Таким образом, правильная запись вышеуказанного умозаключения будет:

Все люди смертны.

Сократ - человек.

Сократ смертен.

Получение истинных знаний посредством умозаключения возможно, если соблюдаются следующие условия:

1. Посылки умозаключения должны быть связаны по содержанию; если суждения, являющиеся посылками, не связаны по содержанию, то вывод из них невозможен.

Например, из суждений: «Все люди смертны» и «Некоторые студенты хорошо учатся» нельзя сделать вывода, так как эти суждения не имеют общего содержания, логически не связаны друг с другом.

2. Посылки умозаключения должны быть истинными суждениями. Если суждения, являющиеся посылками, ложны, то и заключение, как правило, будет ложным. Истинное заключение может получиться лишь чисто случайно.

Например: «Чем больше книг читаешь, тем глупее становишься»

(Мао Цзэдун). «Чем ты глупее, тем лучше живешь»

(Эразм Роттердамский).

«Чем больше книг читаешь, тем лучше живешь».

3) В процессе рассуждения следует соблюдать

правила вывода, которые обусловливают логическую правильность умозаключения. В противном случае из истинных посылок можно получить неверное заключение. Например:

Все студенты - люди.

Ни один профессор не является студентом.

Ни один профессор не является человеком.

Виды умозаключения выделяют по нескольким критериям:

1. По строгости вывода различают умозаключения демонстративные (необходимые) и недемонстративные (правдоподобные).

Демонстративные умозаключения - это

умозаключения, в которых заключение следует с необходимостью из посылок.

Недемонстративные умозаключения - это

умозаключения, в которых правила вывода обеспечивают только вероятностное следование заключения из посылок, а потому выводное знание носит лишь правдоподобный, вероятностный характер. Сравним, например, два умозаключения:

(1) Все противоправные действия караются законом.

Кража - противоправное действие.

Кража карается законом.

(2) Если идет дождь, то земля мокрая. Земля мокрая.

Вероятно, идет дождь.

Первое из этих умозаключений является демонстративным, так как заключение тут с необходимостью следует из посылок. Второе умозаключение не обеспечивает достоверного вывода: земля может быть мокрой по разным причинам, поэтому заключение носит лишь вероятностный характер.

2. По структуре умозаключения выделяют полные, сокращенные и сложные умозаключения. Полным называется умозаключение, в котором есть все необходимые структурные элементы. Сокращенным (или энтимемой) называется умозаключение, в котором пропущена одна из посылок. Например:

Кража - противоправное деяние.

Кража карается законом.

В этом умозаключении опущена как общеизвестное положение посылка: «Все противоправные деяния караются законом». Надо сказать, что в общении мы чаще всего используем сокращенные умозаключения, и только, когда чувствуем ошибочность собственных выводов, восстанавливаем умозаключение до полной формы, чтобы добиться более логически строгого рассуждения и избежать ошибок.

Сложным (или полисиллогизмом) называется соединение нескольких простых умозаключений, в котором заключение одного умозаключения становится посылкой другого. Например:

Всякое общественно опасное деяние наказуемо.

Преступление - общественно опасное деяние.

Преступление наказуемо. Кража - преступление.

Кража наказуема.

Различают прогрессивный полисиллогизм, в котором заключение предыдущего умозаключения (просиллогизма) является первой (большей) посылкой последующего умозаключения (эписиллогизма).

Регрессивный полисиллогизм - это умозаключение, в котором заключение предыдущею умозаключения (просиллогизма) является меньшей (второй) посылкой последующего умозаключения (эписиллогизма).

Приведенный выше пример полисиллогизма является прогрессивным полисиллогизмом.

Примером регрессивного полисиллогизма, может быть, следующий:

Преступления в сфере экономики ~ общественно опасное деяние.

Незаконное предпринимательство - преступление в сфере экономики.

Незаконное предпринимательство - общественно опасное деяние.

Общественно опасные деяния наказуемы.

Незаконное предпринимательство - общественно опасное деяние.

Незаконное предпринимательство наказуемо.

На практике часто используются именно энтимемы и полисиллогизмы, а также их сочетания:

1) эпихейрема - сокращенный полисиллогизм, в котором каждая из посылок представляет собой сокращенное умозаключение (энтимему).

Например:

Ложь заслуживает презрения, так как она безнравственна.

Лесть есть ложь, так как она есть умышленное искажение истины.

Лесть заслуживает презрения.

2) Сорит (полиэнтимема) - сокращенный полисиллогизм, в котором опущена, но подразумевается большая или меньшая посылки (промежуточные заключения).

3. По направленности логического вывода, то

есть по характеру связи между знанием различной степени общности, выраженному в посылках и заключении - выделяют 3 вида умозаключений:

1. дедуктивные умозаключения (от общего знания к частному),

2. индуктивные умозаключения (от частного знания к общему),

3. умозаключения по аналогии (от частного знания к частному).

Эта классификация будет положена в основу дальнейшего изложения.

17. Непосредственное умозаключение

Непосредственные умозаключения являются разновидностью дедуктивных умозаключений.

Дедуктивным умозаключением или дедукцией (от лат. deductio - «выведение») называется умозаключение, в котором переход от общего знания к частному является логически необходимым. Заключение в таком умозаключении, как правило, следует с логической необходимостью (вытекает) из посылок, оно ими обосновано полностью и однозначно.

По существу дедуктивные умозаключения дают чисто формальные выводы, то есть раскрывают в новой форме информацию, изначально заложенную в посылках. Тем не менее, они играют важную роль в науке и практической деятельности, без них невозможно рассуждение. Правила дедуктивного умозаключения определяются характером посылок, которые могут быть в разном количестве и выражены разными видами суждений.

Непосредственные умозаключения - это

дедуктивные выводы из одной посылки, выраженной простым категорическим суждением. Тут суждение, содержащее новое знание, может быть получено непосредственно из исходного суждения, рассматриваемого как посылка. Построение такого вида умозаключений возможно двумя способами:

1. Первый способ построения

непосредственного умозаключения - с помощью логических операций с простыми суждениями, то есть с помощью операций превращения, обращения, противопоставления предикату и противопоставления субъекту, которые уже были нами рассмотрены ранее (п. 3.4.).

Выводы в каждом из этих умозаключений получаются в соответствии с логическими правилами, которые обусловлены видом суждения - его количественными и качественными характеристиками - и правилами операций, с помощью которых преобразуется исходное суждение.

Например, требуется построить все возможные непосредственные умозаключения из суждения: «Все студенты нашей группы (S) являются студентами МИИТа (Р)». В логической форме это суждение имеет вид: «Все S есть Р».

1) Используя операцию превращения, мы получаем непосредственное умозаключение:

Все S есть Р

Все S не есть не-Р

Языковое выражение данного непосредственного умозаключения:

Все студенты нашей группы являются студентами

МИИТа

Все студенты нашей группы не являются не студентами МИИТа

Непосредственные умозаключения, полученные посредством операции превращения, уточняют наши знания. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного суждения, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на свойстве, не совместимом со свойством, выраженным в предикате исходного суждения. В этом смысл данного непосредственного умозаключения и потому оно содержит новое знание о предмете.

2) Используя операцию обращения, мы получим непосредственное умозаключение:

Все S есть Р

Некоторые Р есть S

или в языковом выражении:Некоторые студенты МИИТа являются студентами

нашей группы

3) Используя операцию противопоставления предикату (о правилах этой операции см. 3.4.), мы получаем непосредственное умозаключение

Все S есть Р

Ни одно не-Р не есть S

Или, в языковом выражении, это непосредственное умозаключение имеет вид:

Все студенты нашей группы являются студентами

МИИТа

Ни один не студент МИИТа не является студентом нашей группы.

4) Используя операцию противопоставления субъекту, мы получаем непосредственное умозаключение:

Все S есть Р

Нек. Р не есть не S

В языковом выражении это непосредственное умозаключение имеет вид:

Некоторые студенты МИИТа не являются не студентами нашей группы.

Непосредственные умозаключения, построенные с помощью операций обращения, противопоставления предикату и противопоставления субъекту, уточняют наши знания о предмете и несут новое знание о нем, которое не было явно выражено в исходном суждении.

Часто нам приходится иметь дело с уже сформулированными непосредственными

умозаключениями или выводами из них. В этом случае необходимо проверить правильность вывода. Для этого необходимо установить, какая логическая операция использовалась для вывода и проверить правильность этой операции, то есть удостовериться, что все правила операции были выполнены.

Например, необходимо определить правильность следующего непосредственного умозаключения:

«Ни один человек (S) не рождается специалистом (Р). Значит, все люди (S) рождаются неспециалистами (не-Р)». Логическая схема данного умозаключения:

Ни одно S не есть Р

Все S есть не-РОчевидно, что в данном случае была проведена логическая операция «превращения», и все правила операции выполнены. Следовательно, непосредственное умозаключение верно.

Следует иметь в виду, что логический анализ непосредственного умозаключения начинают с посылки, где определяются два основных термина S и Р. Затем эти же термины обозначаются в заключении. В случае, если понятие заменяется на противоречащее, то ставится и соответствующий символ: не-S или не-Р.

2. Второй способ построения

непосредственного умозаключения - по логическому квадрату.

Зная свойства логических отношений между основными категорическими суждениями А, Е, I, О, которые проиллюстрированы схемой «логического квадрата», можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения.

Например, отношение между противоречащими суждениями (отношение контрадикторности) А и О, Е и I состоит в том, что они не могут быть одновременно ни истинными, ни ложными. Следовательно, из истинности одного суждения следует ложность другого, и наоборот.

На этом основании мы можем построить непосредственное умозаключение:

Все врачи (S) имеют медицинское образование (Р).

Неверно, что некоторые врачи (S) не имеют медицинского образования (Р).

Логическая схема данного непосредственного умозаключения:

Все S есть Р

Неверно, что нек. S не есть Р

Аналогично можно строить непосредственные умозаключения и на основе отношений подчинения, противоположности (контрарности), частичной совместимости (субконтрарности). Выводы можно строить и в том случае, если известно, что исходное суждение ложно. Например, по отношению подчинения между суждениями А и I, Е и О, следует, что из ложности частного суждения следует ложность общего суждения. На этом основании мы можем построить непосредственное умозаключение:

Неверно, что некоторые студенты (S) не являются учащимися (Р).

Неверно, что все студенты (S) не являются учащимися

(Р)-

18. Простой категорический силлогизм.

Простой категорический силлогизм (от греч. - «выведение следствия», «умозаключение») - форма дедуктивного опосредованного умозаключения, в котором из двух категорических суждений (двух посылок) выводится новое категорическое суждение (заключение). Правила такого вывода были определены еще Аристотелем и долгое время служили образцом логической теории.

В логической структуре простого категорического силлогизма понятия называются терминами силлогизма. Различают больший, меньший и средний термины силлогизма.

Меньший термин (обозначается символом S) - это понятие, которое в заключении является субъектом суждения. Посылка, содержащая этот термин, также называется меньшей посылкой.

Больший термин (обозначается символом Р) - это понятие, которое в заключении является предикатом суждения. Посылка, в которой присутствует это понятие в качестве одного из терминов суждения, называется большей посылкой. Меньший и больший термины называются крайними терминами силлогизма.

Средний термин силлогизма (обозначается символом М) - это понятие, которое входит в обе посылки и отсутствует в заключении. Средний термин связывает два крайних термина и обе посылки, и благодаря ему возможен вывод в умозаключении.

Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую посылку, как правило, на первом месте, меньшую - на втором; под чертой записывают заключение. Однако этот порядок может и нарушаться, если из двух уже данных посылок предстоит сделать вывод.

Логический анализ простого категорического силлогизма начинают с заключения, в структуре которого выделяют субъект и предикат суждения; в структуре простого категорического силлогизма они выполняют роль меньшего (S) и большего (Р) терминов силлогизма. Затем соответствующие термины находят в

посылках и определяют понятие, которое является средним термином данного силлогизма (М). Например:

М

Все преступления наказуемы

М

S

Некоторые неумышленные действия являются

S

преступлениями

Р

Некоторые неумышленные действия наказуемы.

В этом силлогизме меньшим термином (S) является понятие «неумышленные действия», большим термином (Р) - понятие «наказуемы», а средним термином (М) - понятие «преступления». В логической форме этот силлогизм можно записать следующим образом:

Все М есть Р Нек. S есть М

Нек. S есть Р

Правомерность вывода, то есть логического перехода от посылок к заключению, в простом категорическом силлогизме основывается на положении (аксиоме силлогизма): все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса.

Р

В данном примере - все, что утверждается относительно всех преступлений, утверждается и относительно

некоторой части преступлений - неумышленных преступлений.

м ММ м

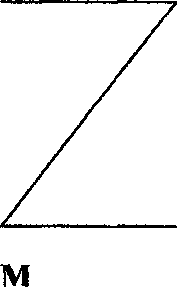
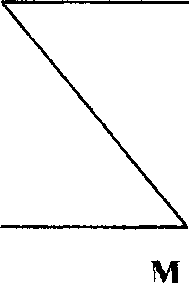
Рис.15

В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката. В зависимости от этого различают четыре фигуры силлогизма. Фигуры силлогизма - это разновидности силлогизма в зависимости от местоположения среднего термина в посылках. Схематически они представлены на (рис. 15), где слева направо изображены 1, 2, 3 и 4 фигуры простого категорического силлогизма.

В первой фигуре средний термин занимает место субъекта в первой посылке (как правило, это большая посылка) и место предиката во второй посылке. Например, вышеприведенный пример простого категорического силлогизма построен именно по первой фигуре:

М- Р S -м

Первая фигура считается основной, так как является наиболее типичной формой дедуктивного умозаключения: из общего положения делается вывод об отдельном случае.

Во второй фигуре средний термин занимает место предиката (то есть второго термина) в обеих посылках. Например:

19. Индуктивное умозаключение

Познание в любой области науки и практики начинается с эмпирического познания. В процессе наблюдения однотипных природных и социальных явлений фиксируется внимание на повторяемости у них определенных признаков. Устойчивая повторяемость наводит на мысль, «индуцирует», что каждый из таких признаков является не индивидуальным, а общим, присущим всем явлениям определенного класса. Логический переход от знания об отдельных явлениях к знанию общему совершается в этом случае в форме индуктивного умозаключения.

Индуктивное умозаключение или индукция (от лат. inductio — «наведение») - это умозаключение, в котором делается логический переход от знания частного к знанию общему, к обобщающему выводу. В индуктивном умозаключении на основании принадлежности признака отдельным предметам или части некоторого класса предметов делают вывод о принадлежности этого признака всему классу предметов в целом. По своему содержанию и познавательному значению эти обобщения могут носить различный характер - от простейших обобщений повседневной практики до эмпирических обобщений в науке и различной профессиональной деятельности.

В истории науки, например, опытным путем было установлено, что железные стержни хорошо проводят электрический ток. Такое же свойство было обнаружено у медных стержней и у серебряных. Учитывая принадлежность указанных предметов к металлам, было сделано индуктивное обобщение, что всем металлам свойственна электропроводность. Это индуктивное умозаключение можно записать следующим образом:

Железо - электропроводно.

Медь - электропроводна.

Серебро - электропроводно.

Железо, медь, серебро - металлы.

Вероятно, все металлы электропроводны.

В индукции заключение не вытекает из посылок с необходимостью, и истинность посылок не гарантирует истинности выводимого из них утверждения. Получаемое в индукции заключение носит, как правило, вероятностный характер. Однако, полнота и законченность опыта влияют на строгость логического следования в индукции, предопределяя ее демонстративный или

недемонстративный характер.

В зависимости от полноты и законченности эмпирического исследования различают два вида индуктивных умозаключений: полную и неполную индукцию.

Полная индукция - это такое умозаключение, в котором общий вывод получается в результате изучения всех предметов определенного класса.

Например: в группе 25 студентов; каждый из них сдал экзамен по логике. Следовательно, можно сделать вывод, что все студенты группы сдали экзамен по логике. Заключение в полной индукции носит не вероятностный, а достоверный характер, поэтому данный вид индуктивного умозаключения является демонстративным

умозаключением.

Познавательная роль полной индукции проявляется в формировании нового знания о классе или роде явлений. Логический переход признака с отдельных предметов на класс в целом не является простым суммированием. Знание о классе явлений - это обобщение, представляющее собой новую ступень познания. Данный вид индукции по обоснованности близок к дедуктивному умозаключению. Однако применять полную индукцию можно лишь в тех случаях, когда число элементов класса - конечно и легко - обозримо.

Неполная индукция - это умозаключение, в котором общий вывод о признаках, присущих всему классу предметов, делается на основе исследования лишь части предметов данного класса. Логический переход в неполной индукции от некоторых ко всем элементам или частям класса не является произвольным. Он опирается на объективную зависимость между повторяемостью признаков и их необходимостью. Отсюда широкое применение неполной индукции в практике.

Однако повторяемость признака может оказаться простым совпадением. Поэтому полученное в неполной индукции знание носит лишь вероятностный характер, то есть неполная индукция - недемонстративное умозаключение.

Степень вероятности заключения в неполной индукции может быть различной. Существенное влияние на характер логического следования в выводах неполной индукции оказывает способ отбора исходного материала, который проявляется в формировании посылок индуктивного умозаключения.

По способу отбора материала различают два вида неполной индукции: популярная индукция и научная индукция.

Популярная индукция (индукция через простое перечисление) - это обобщение, которое делается на основании повторяемости одного и того же признака у ряда однородных предметов. Здесь факты берутся без всякого методического отбора - в результате простого наблюдения того, что встречается в опыте. Главным условием логического вывода в популярной индукции является отсутствие противоречащих случаев. Вывод в этом виде умозаключений проблематичный и обладает малой степенью вероятности, так как противоречащие случаи могли чисто случайно не попасть в поле зрения исследователя.

Тем не менее, этот вид индукции достаточно широко применяется в практике: в метеопрогнозах, в определении причин и прогнозировании эпидемий, прогнозировании поведения людей, в судебно- следственной практике и т.д. Например, лица, совершившие преступления, стремятся скрыться от следствия; угроза убийством часто приводится в исполнение и т.п.

Механизм, который лежит в основе логического вывода, следующий: повторяющийся признак у некоторых явлений наводит на мысль о том, что повторяемость признака - результат не случайного стечения обстоятельств, а проявление каких-то не выявленных закономерностей.

Обоснованность выводов в популярной индукции определяется, главным образом, количественным показателем: чем больше элементов класса исследованы, тем больше степень вероятности индуктивного вывода.

Научная индукция (индукция через отбор фактов) - это умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств. Методика отбора фактического материала в определенной мере исключает случайность обобщения. Факты берутся наиболее типичные, планомерно отобранные. Поэтому вывод обладает достаточно большой степенью вероятности, большой надежностью. Многое здесь зависит от:

(1) числа изучаемых случаев (чем обширнее база индукции, тем более правдоподобным является заключение);

2. от разнообразия, разнотипности обобщаемых случаев;

3. от характера связей между предметами и их признаками, то есть доказательства неслучайности наблюдаемой регулярности.

В зависимости от способов исследования различают селективную индукцию и элиминативную индукцию.

Селективная индукция (индукция методом отбора) - это умозаключение, в котором вывод основывается на знании образца, полученного методичным отбором явлений из различных частей класса предметов. Если в популярной индукции исходят из предположения о равномерном распределении признаков в классе предметов, то в научной индукции класс предметов рассматривается как неоднородное множество с неравномерным распределением признаков в различных его частях. Поэтому образец, необходимый для индуктивного обобщения, формируется по определенным методикам с целью максимально разнообразить условия наблюдения: в образец должны быть отобраны элементы из разных частей класса для того, чтобы были учтены их специфические особенности - в этом случае образец является представительным (репрезентативным).

Элиминативная индукция (индукция методом исключения) - это система умозаключений, в которой выводы опираются на анализ причинных связей в исследуемых явлениях.

Причинной связью называется такая связь между двумя явлениями, когда одно из них (причина) предшествует и вызывает другое (следствие). В истории науки были разработаны специальные методы установления причинных связей. Большой вклад в развитие этих индуктивных методов внесли Ф.Бэкон и Дж.С.Милль.

К индуктивным методам относятся:

1) Метод сходства (метод нахождения сходного в различном). По этому методу сравнивают несколько случаев, в каждом из которых исследуемое явление (а) наступает. При этом все случаи сходны в одном (А) и различны во всех других отношениях (В, С, М, К, D, Р).

Основное правило этого метода: если несколько случаев исследуемого явления возникает в различных условиях, но при наличии единственного общего обстоятельства, то это обстоятельство и есть причина данного явления. Схема рассуждения по этому индуктивному методу может быть записана в логическом выражении, где А, В, С, М, К, D, Р - предшествующие обстоятельства; а - возникающее исследуемое явление.

Случай 1. ABC — вызывает а Случай 2. АМК - вызывает а Случай 3. ADP - вызывает а

Вероятно, А является причиной а

2) Метод различия (метод нахождения различного в сходном). Этот метод применяется тогда, когда рассматриваются два случая, различающиеся тем, что в первом случае исследуемое явление (а) наступает, а во втором - оно не наступает. При этом второй случай отличается от первого лишь одним обстоятельством (А), а все другие обстоятельства сходны. Основное правило данного метода: если при одних и тех же условиях наличие какого-либо обстоятельства вызывает, а его отсутствие устраняет исследуемое явление, то это обстоятельство и есть причина данного исследуемого явления. Схема рассуждения по этому индуктивному методу может быть представлена в следующей форме:

Случай1. АВСК - вызывает а Случай 2. ВСК - не вызывает а

Вероятно, А является причиной а

3) Метод сходства и различия. Этот метод представляет собой комбинацию первых двух методов, когда путем анализа множества случаев обнаруживают как сходное в различном, гак и различное в сходном. Основное правило этого метода: если в одном ряде случаев (1,2,3) исследуемое явление (а) возникает в различных условиях, при наличии одного общего обстоятельства (А), а в другом ряде случаев (4,5,6) то же явление (а) не возникает в сходных условиях, но при отсутствии указанного обстоятельства (А), то это обстоятельство (А) и есть причина исследуемого явления.

Схема рассуждения по этому методу может быть представлена в следующей форме:

СлучайI. ABC-вызывает а

Случай 2. АМК - вызывает а

Случай 3. АРЕ - вызывает а

Случай 4. ВС - не вызывает а

Случай 5. МК - не вызывает а

Случай б. РЕ - не вызывает а

Вероятно, А является причиной а

4) Метод сопутствующих изменений. Этот метод применяется при анализе случаев, в которых имеет место видоизменение одного из предшествующих обстоятельств (А), сопровождаемое видоизменением исследуемого явления (а). Основное правило этого метода: если при изменении предшествующего обстоятельства изменяется и изучаемое явление, а все остальные предшествующие обстоятельства остаются

неизменными, то это изменяемое обстоятельство и есть причина изучаемого явления. Схема рассуждения по этому методу может быть представлена в следующей форме:

Случай 1. АВ С (1) вызывает а (1) Случай 2. АВ С (2) вызывает а (2) Случай 3. АВ С (3) вызывает а (3)

Случай п. АВ С (п) вызывает а (п)

Вероятно, С является причиной а

5) Метод остатков. Этот метод применяется для установления причины, вызывающей часть сложного явления, когда причины, вызывающие все другие части этого явления, уже известны. Основное правило этого метода: если известно, что причиной исследуемого явления не служат необходимые для него обстоятельства, кроме одного, то это одно обстоятельство и есть причина данного явления. Схема рассуждения по данному методу может быть представлена в следующей форме:

1. ABC вызывает авс

2. А вызывает а

3. В вызывает в

Вероятно, С является причиной с Рассмотренные методы установления причинных связей чаще всего применяются не изолированно, а в сочетании, дополняя друг друга. Степень вероятности заключения в научной индукции очень высока.

20. Умозаключение по аналогии

В науке и практических делах объектом исследования нередко выступают единичные, неповторимые по своим индивидуальным характеристикам события, предметы и явления. При их объяснении затруднено применение как дедуктивных, так и индуктивных рассуждений. В этом случае прибегают к третьему способу рассуждения - умозаключению по аналогии.

Умозаключение по аналогии (от греч. analoqia - соответствие, сходство) это умозаключение о принадлежности определенного признака исследуемому единичному предмету на основе его сходства в существенных чертах с другим уже известным единичным предметом.

Например, планеты Марс и Земля во многом сходны: они расположены рядом в Солнечной системе, на обеих есть вода и атмосфера и т.д.; на Земле есть жизнь; поскольку Марс похож на Землю с точки зрения условий, необходимых для существования живого, можно сделать вывод, что на Марсе также имеется жизнь. Это заключение является, очевидно, только правдоподобным, вероятностным.

Умозаключению по аналогии всегда предшествует операция сравнения двух предметов, которая позволяет установить сходства и различия между ними. При этом для аналогии требуются не любые совпадения, а сходства в существенных признаках при несущественных различиях. Именно такие сходства служат основой для уподобления двух предметов.

Аналогия не является произвольным логическим построением, в ее основе лежат объективные свойства и отношения предметов реальной действительности. Каждый конкретный предмет, обладая множеством признаков, представляет не случайную их комбинацию, а определенное единство, целостность, все элементы которой взаимосвязаны.

Общее правило: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других, обнаруженных в одном из сравниваемых предметов, признаках.

Схему рассуждения в умозаключении по аналогии можно представить в следующей форме, где А и В - два единичных предмета; а, Ъ, с, d- их признаки:

А присущи признаки а, Ь, с, d В присущи признаки а, Ь, с

Вероятно, В присущ признак d

Выделяют несколько видов аналогии.

1. По характеру уподобляемых объектов различают аналогию предметов и аналогию отношений.

Аналогия предметов - умозаключение, в котором объектом уподобления выступают два сходных единичных предмета, а переносимым признаком - свойства этих предметов.

Аналогия отношений - умозаключение, в котором объектом уподобления выступают сходные отношения между двумя парами предметов, а переносимым признаком - свойства этих отношений. Следует иметь в виду, что в этом виде аналогии, сами предметы не сравниваются и даже могут не допускать уподобления. Аналогия отношений лежит в основе метода моделирования, который широко применяется в науке и технике. В этом случае экспериментально изученные отношения между параметрами модели (которая может иметь природу, отличную от исследуемого объекта) переносятся на реальный объект.

2. В зависимости от степени достоверности заключения выделяют три вида аналогии: строгую, нестрогую и ложную аналогию.

Строгая аналогия - умозаключение по аналогии, которое опирается на знание необходимой условной связи между переносимым признаком и признаками сходства. Основное правило: если между переносимым признаком и признаками сходства существует необходимая условная зависимость, то это достаточное основание для умозаключения по аналогии, и это будет демонстративное умозаключение, то есть заключение будет достоверным знанием. Схему рассуждения в строгой аналогии можно представить в следующей форме:

А присущи признаки а, Ъ, с, d В присущи признаки а, Ь, с а, Ь, с —» d

В присущ признак d

Нестрогая аналогия - умозаключение по аналогии, в котором зависимость между сходными и переносимым признаком мыслится как необходимая лишь с большей или меньшей степенью вероятности. Вывод носит проблематичный характер.

Для повышения степени вероятности заключений в нестрогой аналогии следует выполнять ряд правил:

1. число общих признаков должно быть возможно большим;

2. сходные признаки должны быть существенными;

3. общие признаки должны быть по возможности более разнообразными;

4. необходимо учитывать количество и существенность различий.

Ложная аналогия - умозаключение по аналогии, вероятность заключения в котором равна нулю. Как правило, аналогия становится ложной, когда не выполняются вышеуказанные правила. В других случаях ложная аналогия - результат отсутствия фактических знаний о предметах и их свойствах, на основании которых аналогия осуществляется.

Например, на ложной аналогии были построены рассуждения одного из сотрудников известного русского физиолога И.П. Павлова, который при анализе опытов, проводившихся на собаках, провел аналогию между внутренним миром людей и воображаемым «внутренним миром» собаки. При этом он не учел, что между человеком и животным существует принципиальное различие, делающее подобную аналогию невозможной: сознание человека качественно отличается от психики животных. Ложная аналогия привела к ложному заключению, по словам И.П. Павлова, к фантастичности и научной бесплодности.

Иногда ложная аналогия используется сознательно и умышленно, чтобы ввести противника в заблуждение, и тогда она становится софистическим приемом.

Софизм - это умышленный обман, основанный на нарушении правил языка или логики. Но обман тонкий, завуалированный, так что его не сразу и не каждому удается раскрыть. Цель его - выдать ложь за истину.

Этим софизм отличается от паралогизма как непреднамеренной ошибки в рассуждении, обусловленной нарушением законов и правил логики, их незнанием.