Вопрос12. Полем называется кольцо p, обладающее следующими свойствами:

     VII. (Обратимость умножения) Для любых a и b из P, где a ≠ 0, уравнение ax = b имеет (по крайней мере одно) решение, т. е. существует элемент   такой, что aq = b.

     VIII. P содержит по крайней мере один элемент, отличный от нуля.

Примеры:

2. Множество рациональных чисел.

3.Множество действительных чисел.

4.Множество рациональных чисел

Вопрос13.Множество всех перестановок множества X (то есть биекций X →X) с операцией композиции образуют группу, которая называетсясимметрической группой или группой перестановок X.

Обычно обозначается S(X). Если X = {1, 2,…, n}, то S(X) обозначается через Sn.

Нейтральным элементом в симметрической группе является тождественная перестановка id, определяемая как тождественное отображение:id(x) = x.

Свойства

• При 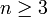  симметрическая группа Sn некоммутативна.

• При 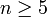  симметрическая группа Sn является неразрешимой.

• В случае, если X конечно, число элементов S(X) равно n! (факториал n), где n — число элементов X.

• Каждая группа G изоморфна некоторой подгруппе группы S(G) (теорема Кэли).

Вопрос14. Кольцо вычетов

Если задано натуральное n, кольцо целых чисел Z разбивается на непересекающиеся классы чисел, имеющих одинаковые остатки при делении на n. Определимсложение и умножение этих классов через операции над их элементами: пустьчисла a и b принадлежат классам A и B соответственно, тогда классы A + B иA × B — это те классы, которые содержат числа a + b и a × b соответственно.

Не трудно проверить, что такое определение корректно. Кроме того множествоклассов с этими операциями образует кольцо, которое называют кольцом Zn вычетов по модулю n.Единичным элементом в нем является класс, содержащий 1,нулевым — содержащий 0.

Пример. Показать, что кольцо Zn вычетов по модулю n будет полем тогдаи только тогда, когда n — простое число.

Решение.

Будем обозначать через Ak класс вычетов, содержащий число k.Если n = p × q, где p и n натуральные числа, большие 1. Тогда Ap × Aq = An = A0,т. е. Aq и Ap — делители нуля, которых не может быть в поле.Если n — простое, то для того, чтобы Zn было полем, необходимо и достаточно,чтобы каждый ненулевой имел обратный. Рассмотрим произвольный Ap (1 < p <n). Все числа p,2p,...,(n − 1)p имеют попарно различные ненулевые остатки приделении на n. По принципу Дирихле, среди них найдется равный 1. Таким образом,

∃k : 1 < k <n,Akp = A1. Но Ap × Ak = Akp. Значит, для Ap существует обратный.

вопрос15. Кольцо вычетов Z_n является полем полем вычетов тогда и только тогда, когда n=p является простым числом.

Доказательство. Если n=p - простое число, то Z_p - кольцо без делителей нуля (действительно, если C_kC_l=C₀,  ,  , то kl=pq, но k и l не делятся на p, что приводит к противоречию). Доказательство завершает следующая лемма.

Кольцо вычетов по модулю 

При описании блочных кодов [25, 30, 33] широко используется понятие кольца вычетов по модулю некоторого полинома   с коэффициентами из поля  .

Для полиномов существуют понятия, аналогичные введенным в 5.8 для чисел, если заменить в этих понятиях слово «число» словом «полином». Так, если при делении полиномов   и   из   на   получаются одинаковые остатки, то многочлены   и   сравнимы между собой по модулю многочлена   из   или  .

Все полиномы, сравнимые между собой по модулю  , образуют класс вычетов по модулю  , а каждый полином класса называется вычетом по модулю  . Каждый класс характеризуется своим представителем, в качестве которого обычно выбирают полином, степень которого меньше степени  . Количество классов вычетов по модулю   равно числу многочленов, степени которых меньше степени  .

Совокупность классов вычетов по модулю   образует кольцо вычетов по модулю  . В качестве операций сложения и умножения в этом кольце используются сложение и умножение по модулю  .

Пример 5.13. Рассмотрим кольцо классов вычетов по модулю полинома   над двоичным полем. Полиномы вида  , где   – произвольный полином, степень которого меньше 2, при фиксированном   образуют класс вычетов по модулю  . Так как всего имеется 4 разных полинома   степени меньше 2, то возможны 4 следующие класса вычетов:

Здесь   – произвольный полином. В качестве представителей классов обычно выбирают вычеты наименьшей степени, которые совпадают с полиномами   и образуют кольцо классов вычетов по модулю полинома  , т.е. множество  .

16. Теорема о числе подмножеств n-элементного множества

Теорема

Любое подмножество конечного множества само конечно. Любое надмножество бесконечного множества само бесконечно.

Если множество содержит конечное число элементов, то говорят, что оно конечно, в противном случае множество называется бесконечным. Число элементов конечного множества A называется мощностью множества A и обозначается |A|. В дальнейшем мы будем различать общий (текущий) элемент x множества A, т.е. произвольный элемент, характеризующийся единственным свойством “принадлежать множеству A”, и конкретные элементы a, b, c каждый из которых отличен от других. Множество A, состоящее из элементов a,b,c,... записывается A={a,b,c,...}.

Обозначим через - число различных k-элементных подмножеств n-элементного множества.

Теорема.

=n!/k!(n-k)!, если k n.

Доказательство теоремы.

Теорему будем доказывать индукцией по k. Базис индукции k=0. Имеем =n!/n!0!=1, что верно, так как 0-элементное множество лишь одно, а именно пустое множество .

Пусть утверждение теоремы верно для любого k, 0 kn-1. Покажем, что теорема верна и для k+1.

Действительно,

=(n-k)n!/(k+1)(n-k)k!=n!/(k+1)!(n-k-1)!,

что доказывает теорему.