6.2 Роль пуассоновского и экспоненциального распределения в тмо

Процесс МО хар-ся след св-ми входных и выходных потоков:

1/вер-ть наступления события (или поступления заявок или выбытия обслуженных) в интервале времени от t до t+h зависит только от величины h , т.е. не зависит ни от кол-ва событий, произошедших до момента t, ни от положения t на оси времени, т.е. рассматривается стационарный процесс. 2.вер-ть наступления события на бесконечно малом отрезке времени h ( 0<h<1) 3. на отрезке времени h реализуется не более одного события

Исп-ся пр выводе формулы вер-ти наступления n- событий в интервале h. В соот-ии с 1 св-ом: события явл равновероятными и статистически независимыми, т.е.n =0 P

В соот-ии со 2-ым св-ом: для бесконечно малого h 0<p (h)<1 P

 - полож. постоянная частота наступления событий

h P

в соот-ии со свойством 3: p

Процесс, описываемый ф-ей P явл случайным, в том смысле, что длина интервала времени, в течение которого происходит каждое последующее событие не зависит от времени, кот понадобится для реализации предшествующего события – свойство отсутствия памяти и хар-на для экспоненциального распределения.

6.3 Моделирование входного и выходного потоков

Входной поток считается процессом «чистого рождения», т.е. поступающие в систему требования обязательно присоединяются к очереди и не покидают систему до тех пор, пока не будут обслужены. Для h->0 и n>0 P

1. n поступлений в течении t- единиц времени и ни одного поступления в интервал h

2. n поступлений в течении t- единиц времени и одно поступление в интервал h

P

h->0

P - решение системы (n=0,1,…)

Распределение вер-ти подчиняется з. Пуассона со средними значениями и дисперсиями равными t

Выходной поток - процесс на выходе системы. Рассматривается предположение, что система начинает функционировать при наличии n – клиентов, кот после завершения обслуживания системы с интенсивностью  выбывают из неё. (процесс чистой гибели)

q - вер-ть того, что в течение t – единиц времени из системы будет изъято n – единиц запасов. как и в случае чистого рождения при условии абсолютной вер-ти исходов для достаточно малого интервала h:

для q :

После тривиальных упрощений и перехода к предельным значениям составляется система ДУ: Рез-т решения этой системы: q n=0,1,...,N-1

Если необ-мо определить вер-ть того, что в системе по истечению t- единиц времени останется n- единиц заявок

p

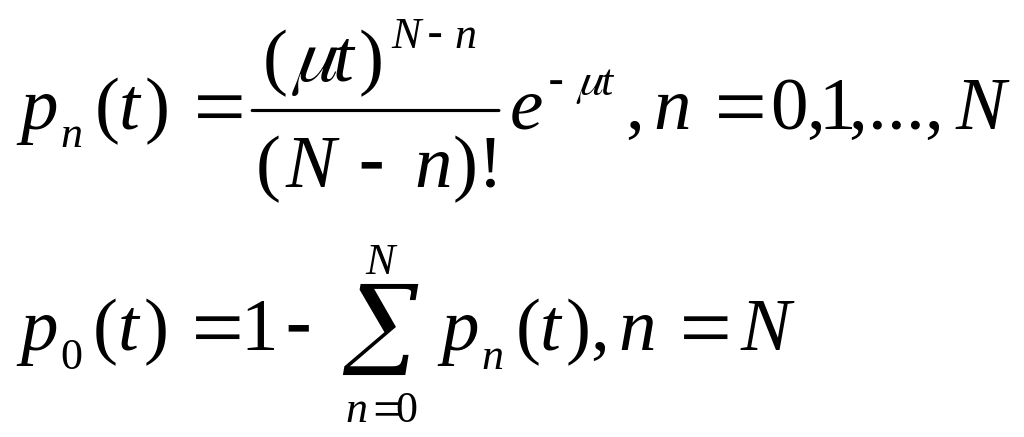
6.4 Смо неограниченной мощности

(M/M/1):(GD/ / )

Основные задачи: 1. необ-мо получить ур-ие для Pn(t) 2. При соот-щих условиях перейти к пределам и получить формулы для Pn(t), соот-щие стационарному режиму процесса.

1. P(число поступлений в интервале h равно 0)=e 2. P(одно поступление в интервал h)= 1-e 3. P( число выбытий в инт h равно 0) = e 4. P( одно выбытие в инт h) =1-e

Далее рассматривается P . Складывается из след вер-ей: 1. Р( в конце инт t нах-ся n- заявок, в инт h - не происходит ни поступлений, ни выбытий) 2. Р( в конце инт t в системе нах-ся n-1- заявка, в инт h происходит 1 поступление, но не происходит выбытий). 3. Р( в конце инт t в системе нах-ся n+1- требований, в инт h не происходит ни одного поступления, но происходит одно выбытие).

Предполагается, что события происходят случайным образом. В инт h происходит не более одного события, т.е. вер-ть реализации 2-х событий равна 0. Далее суммируя три вероятности для n>0 (Ф №1), получаем систему ур-ий ( Ф№2). Их решение позволяет определить Pn(t), кот описывает стохастический процесс (не обязательно явл стационарным).

Если P

ф№3

Сходимость обеспечивается за счет величины . Ф№4. Расчет основных операционных хар-к не зависит от дисциплины очереди, но при этом хотя среднее время ожидания в очереди от дисциплины очереди не зависти распределение продолжительности пребывания в системе зависит от дисциплины очереди.

(M/G/1):(GD/ / )

1. Входной поток пуассоновский с интенсивностью 2. Распределение обслуживания – произвольное со среднем значение E(t) и дисперсией var(t) 3. выполняется условие стационарности при . ф№8

(M/M/C):(GD/ / )

Эквивалентен обслуживанию одним узлом или прибором, быстродействие кот увеличено в m – раз при наличии в системе n- требований. Цель исп-ия неск узлов – повышение скорости обслуживания за счет одновременного обслуживания неск заявок. 1. если n=c, то интенсивность входного потока равна c . 2. если n<c, то заняты обслуживанием не все узлы n <c . Для моделирования исп-ся обобщенная одноканальная модель, в кот интенсивность входного потока и скорость обслуживания зависят от числа заявок n ( и ). Полагая, что = и =n* (n<c) и =c* (n>=c) можно получить оценки для всех операционных хар-к. После нахождения значений вер-ти Pn при заданных и можно получить формулы расчета для систем других конфигураций (например для (M/M/1):(GD/ / )). Обощающая модель: (Мn/Mn/1):(GD/ / ), для кот справедливы следующие утверждения: 1. Р(при наличии в системе n – требований в инт h не происходит ни одного поступления) 2. Р(при наличии в системе n- требований в интервале h не происходит ни одного выбытия) .

Учитывая, что в интервале h не может произойти не более 1 события, то определяют (Ф№9). Для стационарного режима: (Ф№10). Рассматривая последовательно эти уравнения для разных вероятностей Р1, Р2,…, получают формулы для обобщенной модели: (Ф№11). Для оценки операционных хар-к из выражения для вер-ти Pn при n<=c получают ф№12.1, при n>=c – ф№12.2. ф.13, ф.14, ф.15, ф.16, ф.17.При значении

намного меньше 1 получают

(M/M/ ):(GD/ / ) Модель самообслуживания, т.е заявка выступает в роли обслуживающего узла. для авывода формул исп-ся обобщенная одноканальная модель:

ф№24 и ф№25.

Распределение Рn –ой величины яво пуассоновским со средне значением Е(n)=

Для этой модели можно вывести формулы для вер-ти Pn(t) в том случае, когда процесс не явл стационарным. ф№26, т.е. для неустановившегося режима имеет место распределение Пуассона со средне значением E(n)= . Полученные рез-ты можно исп-ть для оценки соот-щих рез-ов, относящихся к модели М/М/С, если С- достаточно большое число. При малых значениях (когда ) аппроксимация будет достаточно точной, даже и для небольших значений С.

(Mi/Gi/1):(NPRP/ / ) - одноканальная модель. Fi(t) – произвольная ф-ия распределения продолжительностей обслуживания из i- ой очереди со среднем значением Ei(t) и дисперсией VARi(t). - для произвольной очереди. Ф№27 Ф№28.

Среднее время прибывания заявки в очереди не зависит от её приоритета и составляет величину Ф№29.

(Mi/Mi/C):(NPRP/ / ) Распределение одинаково для всех требований независимо от категории, подчиняются экспоненциальному распределению со средней скоростью . поступления заявок с любым приоритетом k=1,2..,m подчиняется распределению Пуассона со средней частотой для любой очереди .Ф№30