1)Основные понятия и аксиомы классической кинематики

Кинематика – раздел теоретической механики, в котором механическое движение объектов природы и техники, механические явления и процессы изучаются с «геометрической» стороны, т. е. безотносительно к взаимодействию этих объектов, причине изменения их движения и т. д. Кинематика по-другому назы­вается хроногеометрией (геометрией во времени)

В кинематике строятся математические модели объектов природы и техники, механических явлений и процессов безотносительно к материальному составу этих объектов.

Кинематика – базируется на аксиомах классической евклидовой геометрии, аксиомах о равномерном течении времени и непрерывности движения.

3)Три способа задания движения точки

В кинематике как хроногеометрии движение точки должно быть задано.

А) Векторный способ задания движения точки

В

Рис. 1

екторный способ задания движения вытекает из физических основ механики. Он связан с измерением отрезков и углов (направлений). В силу этого этот способ практически не применяется в ТМ для решения задач. В курсе ТМ к нему обращаются в основном для определения кинематических мер, для записи формул и т. д.

При векторном (физическом) способе задания движения точки ей ставится в соответствие в каждый момент времени ее радиус-вектор относительно некоторого условного неподвижного центра – полюса. Таким образом, радиус-вектор (рис. 1) является непрерывной векторной функцией аргумента t:

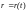. (1)

_{Это означает, что в каждый момент движения точки задаются как величина} r = r(t), так и направлени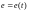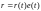е : , где .

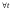Зависимость задает закон движения точки.

У свободно движущейся точки число кинематически независимых движений равно 3: по осям xyz. В связи с этим говорят о 3 степенях свободы (s) движения точки.

s = 1_x + 1_y + 1_z = 3.

Таким образом, движение точки происходит в 3-мерном пространстве ее движений, совпадающем по размерности с 3-мерным пространством вещественных материальных форм, называемом в современной науке просто пространством.

Б) Траектория точки

Точка в пространстве движется по траектории.

Траектория точки есть геометрическое место точек простран­ства, которые последовательно во времени проходит движущаяся точка. Говорят также, что траектория то­чки есть годограф радиуса-вектора

В геометрии под годографом вектора понимают линию, которую описывает его конец. Траектории бывают разомкнутыми и замкнутыми. Разомкнутые имеют начало при t = 0. По замкнутым, как правило, движение происходит по циклу. Заметим, что на разных участках движения траектория может описываться разными уравнениями.

В) Координатный способ

При координатном способе с полюсом связывают какую-либо систему координат. Рассмотрим в качестве примера только декартову и цилиндрическую (полярную) системы координат, рис. 2.

4)Вычисление скорости и ускорения точки при векторном способе задания движения точки.

Из физических основ механики следует, что

5) Вычисление скорости и ускорения точки в декартовых осях

Вычислим скорость точки в декартовых осях, взяв за основу выражения (2), (3), (15) и (16). Тогда

.

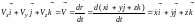Таким образом,

(17)

Аналогично получим выражения для компонент ускорения точки:

, (18)

.

6) Вычисление скорости точки в естественных осях

Вычислим скорость точки в естественных осях на основе (14) и определения (15). Тогда с учетом того, что , получим

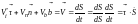(19)

, .

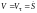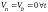Таким образом, скорость точки всегда касательна к ее тра­ектории.

Вычисление ускорения точки в естественных осях

Выведем формулу для вычисления ускорения точки в естественных осях на основе определения (16) и формулы (19). Согласно рис. 6 изменяется по величине и по направлению, изменяется только по направлению:

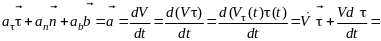
(20)

Рис. 6

В этом случае вычисление производной осуществим на основе рис. 6.

Изобразим элемент траектории точки dS с единичными векторами в моменты t и t + dt. Здесь 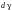– угол смежности. Перенесем вектор параллельно к моменту t. Так как векторы и единичные, то, соединив их концы, получим:

,

где – центр окружности кривизны.

Так как 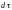зависит от , то

,

(так как , где 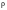– радиус окружности кривизны).

Таким образом,

(21)

и вектор ускорения точки всегда лежит в касательной плоскости и раскладывается на тангенциальное и нормальное направления:

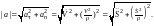(22)