6. Эффективные, минимальные и оптимальные портфели
Пусть задан пакет из n активов, тогда можно сформировать различные портфели из активов выбранного пакета.
Множество
{
/
}
всевозможных портфелей для данного пакета активов называется допустимым множеством.
Каждому портфелю можно поставить в соответствие пару чисел - его ожидаемую доходность и ожидаемый риск (E,V).
Введя координатную плоскость с координатами (E,V), мы можем для каждого портфеля из допустимого множества вычислить E, V и отобразить в этой плоскости точку с координатами E,V. Такая плоскость называется плоскостью оценок, а пара Q=(E,V) оценкой портфеля. Образом допустимого множества при таком отображение будет некоторое множество в плоскости оценок, которое обычно называют критериальным множеством.
Такой портфель, что в допустимом множестве портфелей не найдется портфеля с наибольшей доходностью и наименьшим риском называется эффективным. Очевидно, что оценки эффективных портфелей лежат на границе критериального множества. Множество оценок эффективных портфелей называют эффективной границей критериального множество или кривой Парето.
Если задать уровень доходности Е0, то портфели с уровнем доходности Е0 и минимальным риском называются минимальными (по риску) портфелями. Оценки минимальных портфелей составляют минимальную границу критериального множества.
Эффективная граница является частью минимальной границы критериального множества.
Наилучшим портфелем из заданного множества портфелей будем считать портфель с наибольшей доходностью и наименьшим риском.
Наилучший портфель из множества допустимых портфелей - оптимальный портфель.
Пример 6.1.
Описать допустимое множество портфелей для пакета из двух активов.
Решение
Пакет состоит из двух активов, т.е. n = 2. Допустимое множество
{
/
}
В двумерной плоскости
допустимое множество есть прямая
проходящая через точки (0,1) и (1,0).
Ответ: { / }.
Пример 6.2.
Пусть известны оценки трех портфелей
Q1=(E1,V1)=(1.2;0.5), Q2=(E2,V2)=(2;0.3), Q3=(E3,V3)=(0.4;2).
Найти наилучший портфель среди этих портфелей. Будет ли он эффективным? оптимальным? минимальным?
Решение
Сравним доходности этих портфелей. Второй портфель имеет большую доходность, т. к.
Наименьший риск имеет второй портфель, т. к.
Значит из заданного множества портфелей наилучшим является второй.
Так как нам неизвестно допустимое множество, а значит и критериальное множество в плоскости оценок, то сказать является ли второй портфель минимальным, эффективным или оптимальным мы не можем. Однако ни первый, ни третий портфель не являются эффективными, т. к. в множестве допустимых портфелей есть портфель (второй) имеющий большую доходность и меньший риск.
Ответ: Из заданного множества портфелей наилучшим является второй.
7. Построение критериального множества
Пакет состоит из двух активов -
.
Допустимое множество в этом случае
{ / }.
Пусть характеристики пакета
(
),
Ожидаемая доходность есть
. (7-1)
Ожидаемый риск есть
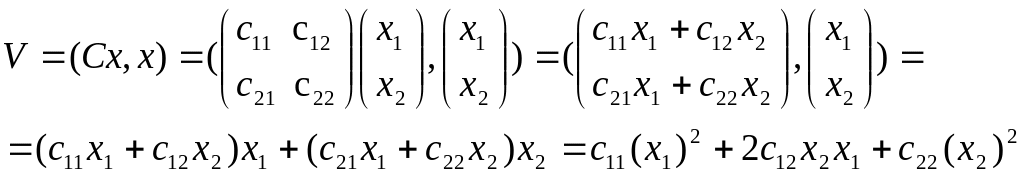-(7-2)
Так как
,
то подставляя
в (7-1)-(7-2) получаем зависимость доходности
и риска от
.
(7-3)
Из (7-3) находим
и подставляем в (7-4)
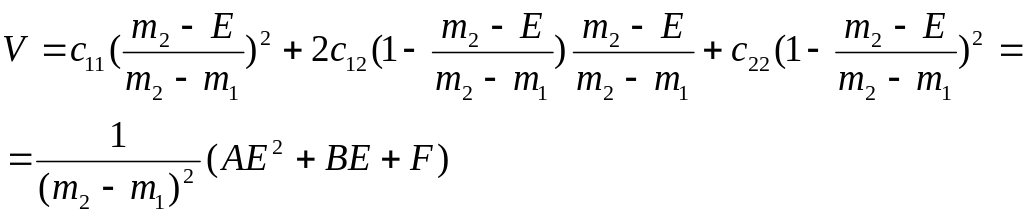
где
Если
минимальная граница критериального
множества есть парабола, если
-
прямая. Критериальное множество будет
внутренняя область параболы, а эффективная
граница - правая ветвь параболы.
Пример 7.1.
Пакет состоит из двух активов - .
Характеристики пакета
,
.
Найти критериальное множество,
эффективную и минимальную границы.
Решение
Вычислим значения коэффициентов A,B,F
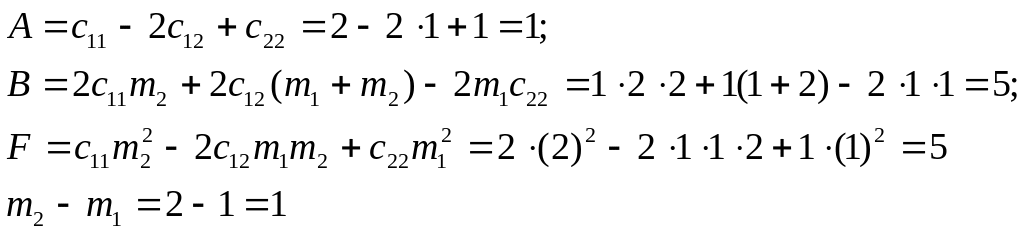
Учитывая полученные результаты получаем
Минимальная граница критериального
множества - парабола, ветви которой
направлены вверх и вершина в точке -
.
Правая ветвь параболы задает эффективную
границу критериального множества.
Критериальное множество внутренняя
часть параболы.
Ответ:
Минимальная граница критериального
множества - парабола
.
Задачи
Найти и построить критериальное множество для пакета активов
7.1. {AMEX, CBS}, 7.2. {EXXON, CBS}, 7.3. {EXXON, AMEX}.
(Воспользуйтесь результатами полученными при решении задач 4.1, 4.2, 4.3)
Найти координату вершины параболы.
7.4. Найти минимальную и эффективную границы критериального множества для задач 7.1, 7.2, 7.3.
7.5. Сравнить полученные результаты и провести анализ.
7.6. Привести пример оценки не эффективного портфеля.
7.7. Привести пример не минимального портфеля.