2. Вынуждающие вибрацию силы

Воздействие потока вызывает вибрацию трубчатки, рассчитать которую часто бывает не просто.Это воздействие вызывает распространение вихрей, упругую неустойчивость жидкости, турбулентную вибра­цию, образование вихря в параллельном потоке, акустиче­скую вибрацию.

Рассмотрим каждый из этих механизмов при образовании вибрации.

Поперечное обтекание трубы вызывает ряд вихрей в спутном следе, образуемых в связи с тем, что поток отрывается попеременно от проти­волежащих частей периметра трубы (рис.8.6.). Это распро­странение вихрей создает переменные силы, частота которых увеличивается по мере возрастания скорости потока. Для одиночного цилиндра диаметр трубы, скорость потока и частота возникновения вихрей могут быть связаны без­размерным числом Струхаля (Sr):

, (8.3.).

Рис. 8.6. Схема образования вихрей при поперечном обтекании трубки.

Для одиночных цилиндров число S_ч, описывающее распространение вихрей, постоянно; значение его приб­лизительно равно 0,2. Вихри возникают в диапазоне чисел Рейнольдса 100 - 510⁵ и при Rе>210⁶ и исчезают при промежуточных значениях Rе. Этот промежуток обуслов­лен сдвигом точки отрыва потока.

Иногда колебания труб, вызванные другими силами могут провоцировать отрыв вихрей от вибрирующей трубки.

Значения числа Струхаля для идеального пучка труб практически постоянны в широком диапазоне чисел Рей­нольдса, но существенно изменяются в зависимости от продольных и поперечных шагов труб. В этих случаях число Струхаля можно определить по эмпирической формуле Жукаускаса:

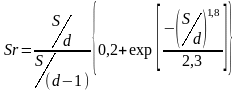(8.4.).

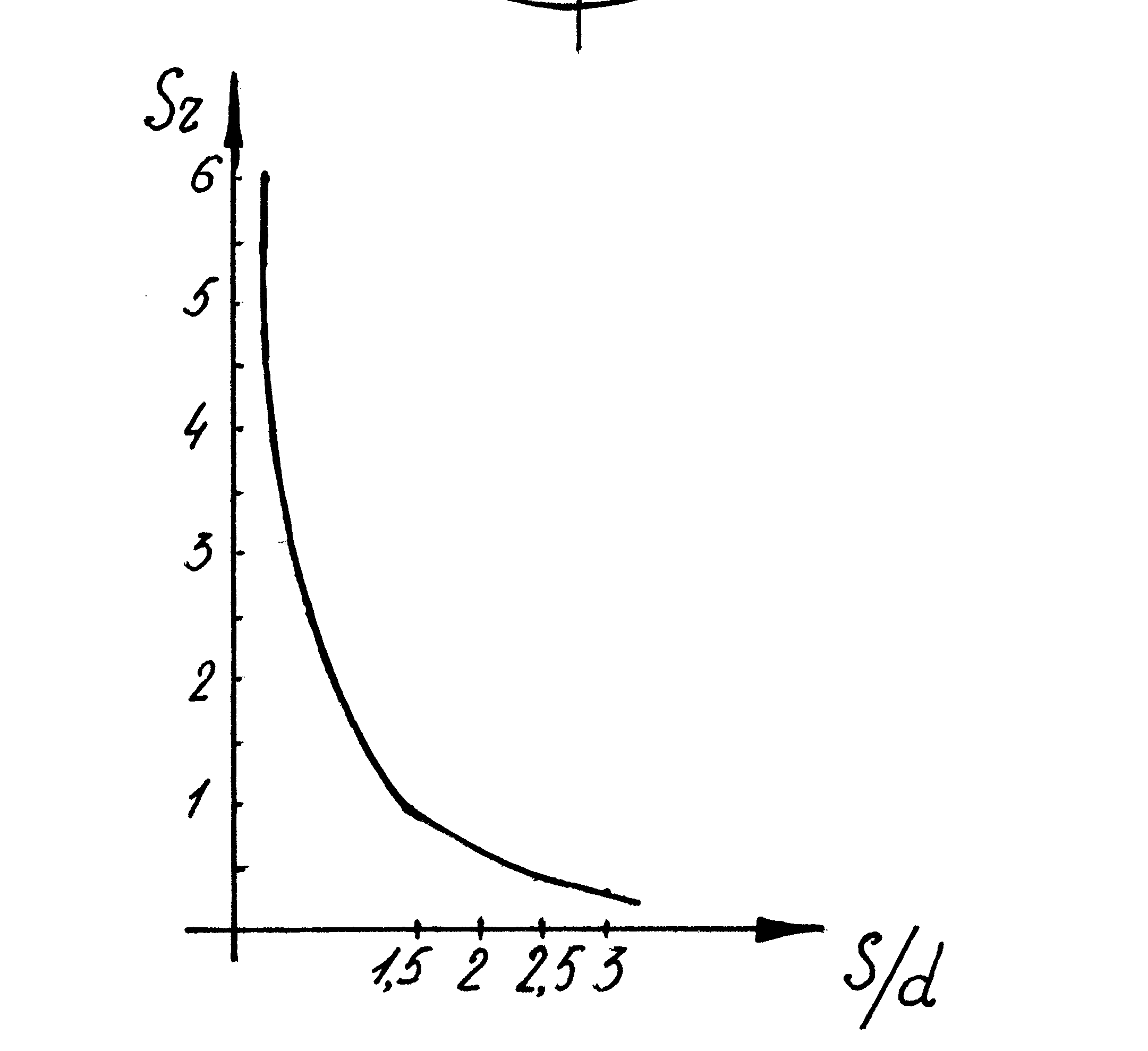
Рис. 8.7. Зависимость критерия Струхаля от относительного шага труб в пучке.

В случае, если поток омывает трубный пучок под углом, можно использовать экспеориментальные данные [ ], представленные на рис.8.8.

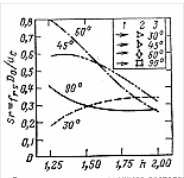
Рис. 8.8. Число Струхаля для равностороннего расположения труб в пучке при разных углах взаимного расположения труб (h – относительный шаг): 1 – поток; 2 – расположение труб; 3 – угол.

Турбулентная вибрация содержит ши­рокий спектр частот, распределенных вокруг основной частоты. Она возрастает по мере роста скорости потока. Любой турбулентный поток характеризуется средним значением скорости V_ср и составляющей пульсаций V_тр:

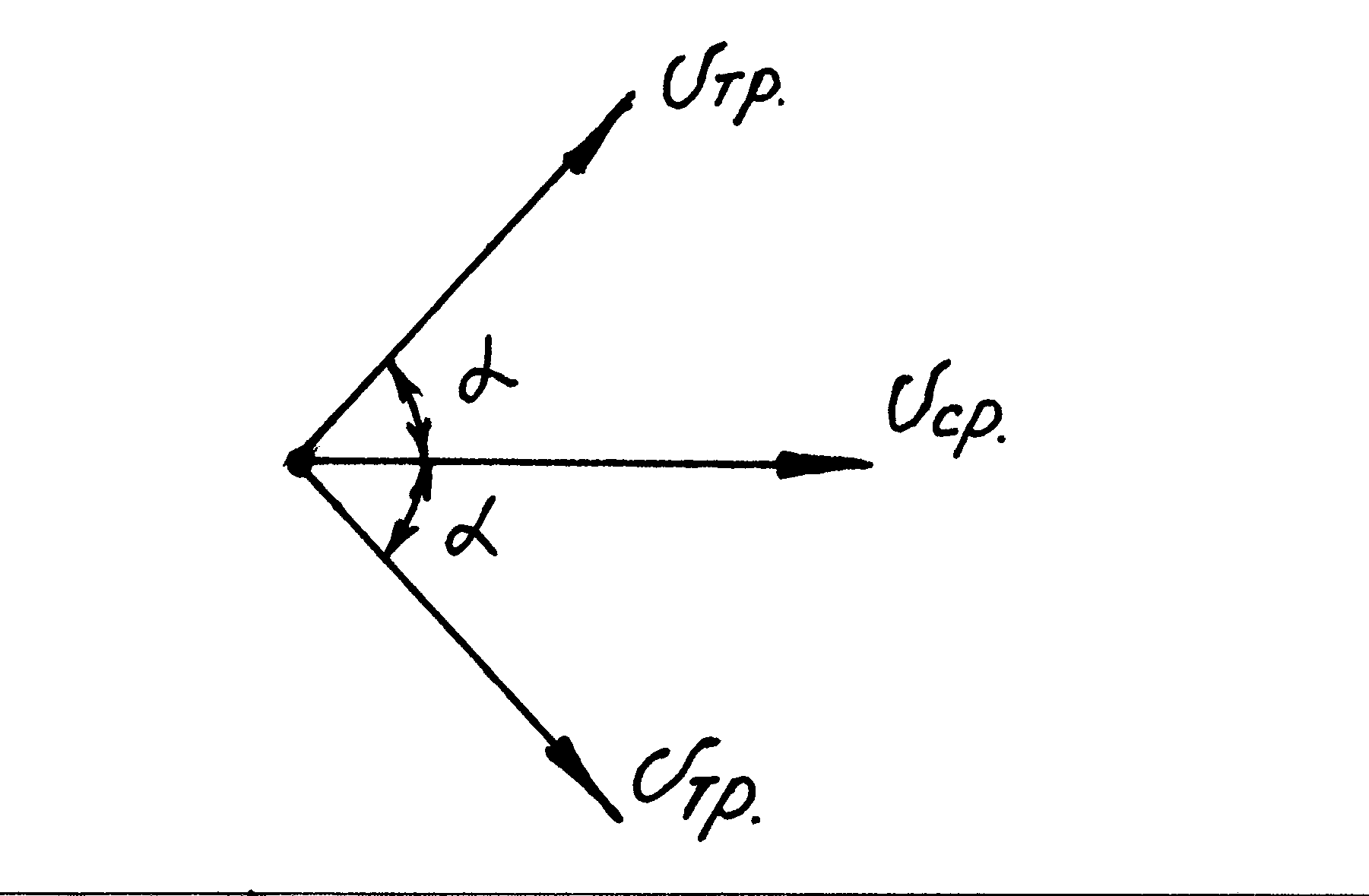
Рис. 8.3. Вращение вектора скорости турбулентных пульсаций

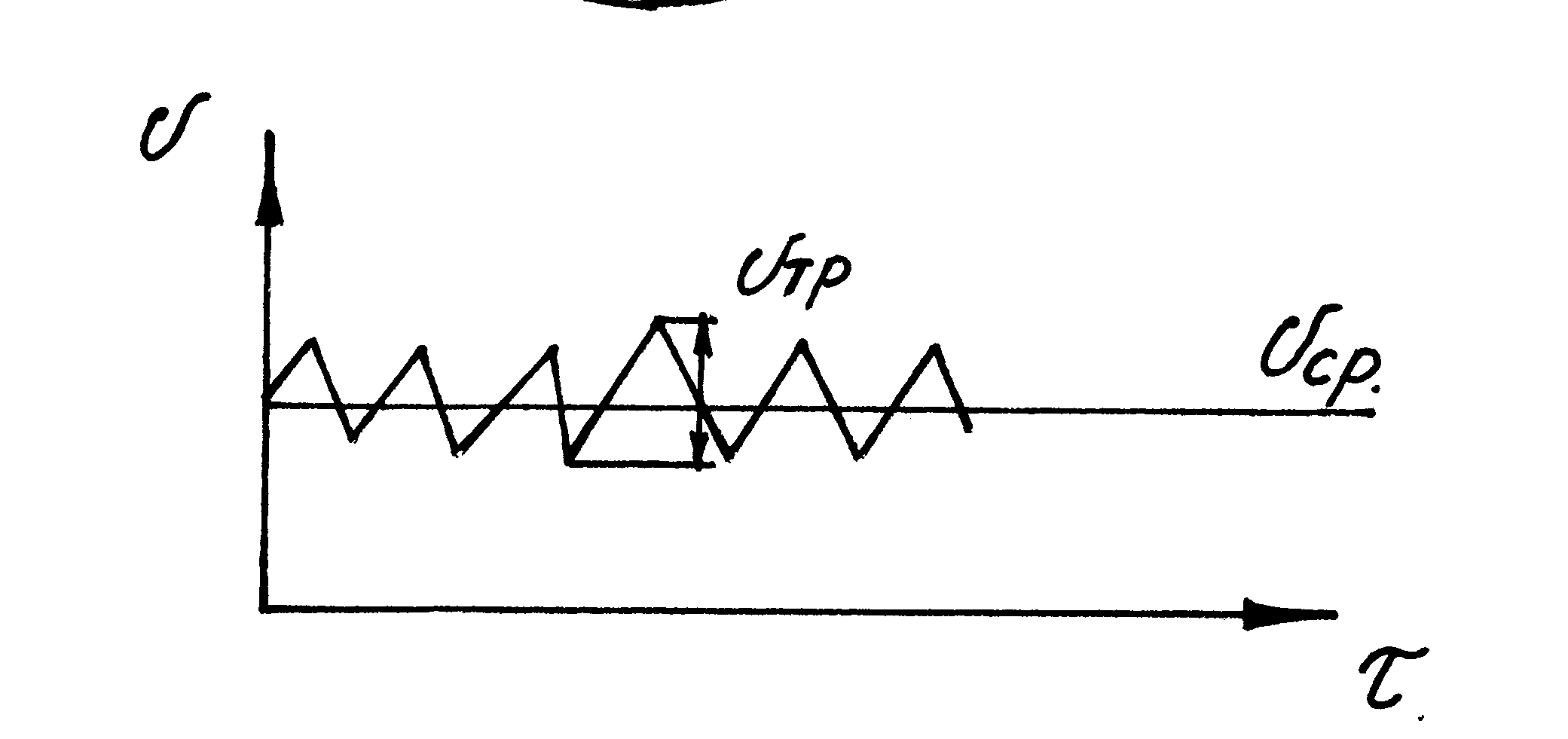
Рис. 8.4. Турбулентные пульсации потока

Турбулентность вызывает вибрацию в трубах, на которые воздействуют отдельные частоты тур­булентного потока. Это чрезвычайно сложная форма воз­буждения. В результате исследований на газе, поперечно обтекающем идеальный пучок труб, в […] было предло­жено эмпирическое уравнение для расчета основной час­тоты турбулентной вибрации.

(8.5.)

где - продольный шаг в трубчатке;

t – поперечный шаг.

Турбулентные пульсации в настоящее время полностью не исследованы, а приведенная формула не пригодна для капельной жидкости.

Помимо турбулентной вибрации основной частоты су­ществуют вибрации с другими частотами и энергиями. Предполагается, что спектр частот турбулентной виб­рации можно представить в виде полосы ±9 Гц (отсчет от основной частоты). В случае когда основная частота турбулент­ных вибраций близка в частоте собственных колебаний, возникают вибрации со значительной амплитудой или резонанс.

Упругие завихрения жидкости обусловлены вибрацией труб при движении, вызываемом поперечным обтеканием труб. Движение со­стоит в продольном и поперечном перемещениях труб на частотах их собственных колебаний. Обычно возникнове­ние упругого завихрения жидкости приводит к выходу труб из строя, в том случае, если подвод энергии превышает количество энергии, которое может рассеиваться затуханием. Предполагается [ ] метод расчета критической скорости поперечёного потока _кр. превышение которой дает упругое завихрение жидкости и может привести к разрушению трубки:

(8.6.)

где  - плотность жидкости;

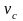- собственная частота колебаний;

 - пороговая постоянная неустойчивости (табличная безразмерная величина; рис.8.12..

Логарифмический дикримент затухания.

Условие устойчивости трубных пучков в зависимости от среды, угла оьтекания, числа Струхаля представлено на рис.8.11.

Параметр затухания М_e _o/ D²_o

Рис. 8.11. Диаграмма устойчивости для рядов труб (согласно [21])

Значение постоянной пороговой неустойчивости , входящей в формулу (8.6.) можно определить по данным, представленным на рис.8.12.

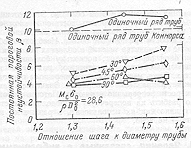
Рис.8.12 Зависимость постоянной пороговой неустойчивости от отношения шага к диаметру трубы при разных углах расположение труб в пучке .

Акустическая вибрация возникает только в том случае, если в межтрубном пространстве находится пар или газ. Вибрации этого типа аналогичны звуковым вибрациям, возникающим в органной трубе. Характерная частота акустической вибрации в теплообмен­нике зависит от некоторой характерной длины (обычно от диаметра кожуха D) и скорости звука теплоносителя u_sound. Акустическая частота _а может быть рассчитана с помо­щью следующего соотношения:

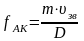(8.7.)

где m — номер моды, который является безразмерным множителем. Самая низкая частота достигается при m = 1. Эта час­тота называется основным тоном; более высокие обертоны имеют акустические частоты в 2—4 раза больше основной (m = 2, 3 или 4). Первые два обертона показаны на рис. 8.13. Возникновение третьего, четвертого и более высоких обер­тонов в теплообменниках наблюдается редко.

Акустические частоты вибраций в теплообменнике могут возбуждаться либо вихрями, либо турбулентными вибрациями. Установлено, что пока возбуждающие частоты лежат в пределах 20% акустической частоты, возникает лишь громкий шум,однако акустическая вибрация может вызывать разрушение в том случае, когда она попадает в резо­нанс с каким-либо элементом теплообменника. Тщательно выполненные проекты теплообменников учитывают, что частоты собственных колебаний труб должны отличаться от акустических частот кожуха теплообменника. Акусти­ческие частоты кожуха можно изменить, вставляя рас­страивающую пластину, расположенную параллельно направлению по­перечного обтекания. Это изменяет характерную длину, а теплоотдача и перепад давления не изменя­ются.

Н аправление потока

Рис. 8.13. Наиболее вероятные формы стоячих акустических волн для основного (1) тона, первого (2) и второго (3) обер­тонов.