10.3. Тепловое подобие

Аналогично гидродинамическому подобию рассмотрим условия теплового подобия. Вначале разберем случай чистой теплопроводности, т. е. переноса тепла молекулярным способом без конвекции. В этом случае уравнение переноса тепла имеет вид

где 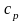— удельная теплоемкость жидкости.

Приведем это уравнение к безразмерному виду, для чего введем следующие безразмерные величины:

где - безразмерные величины; - характерные размерные величины (масштабы).

Рассмотрим одномерное движение, т. е. Т == T(t, x), тогда

Подставив принятые соотношения в уравнение переноса тепла, получим

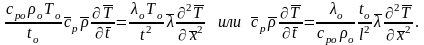
Как было указано ранее, 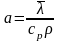называется коэффициентом температуропроводности.

Число, равное , называется числом Фурье. Оно характеризует не стационарность процесса молекулярного переноса.

Далее рассмотрим случай конвективного переноса тепла. Для одномерного установившегося движения соответствующее уравнение имеет вид

.

Введя безразмерные величины, получим

или

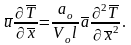
Следовательно, для подобия процессов необходимо соблюдать равенство числа , характеризующего конвективный перенос; обратная величина называется числом Пекле (Ре):

Перенос тепла с поверхности при разности температур в потоке и на стенке T₁ - Т_w, можно представить в виде

где T₁ - температура окружающей среды; Т_w, - температура стенки;  - коэффициент теплоотдачи (теплопереноса).

Для плотности теплового потока имеем

(10.3)

Воспользуемся выражением (10.3) и получим еще одно число подобия. Если уравнение в безразмерном виде

разделим на получим

.

Число называется числом Нуссельта и обозначается Nu,

Так как коэффициент теплоотдачи , входящий в число Nu, меняется от точки к точке, то это число является локальным.

Если в выражение для числа Nu подставить среднее значение коэффициента

то полученное значение будет называться средним значением числа Нуссельта.

Количество тепла, которое снимается со стенки, имеющей длину l и ширину, равную единице, будет

Физически число Nu можно рассматривать как отношение действительного теплового потока, определяемого величиной коэффициента теплоотдачи , к удельному тепловому потоку, который имел бы место в условиях чистой теплопроводности в слое толщиной l, т. е. .

Если разделим число Ре на число Re, то получим число Прандтля Рr:

.

Число Рr характеризует отношение двух характеристик молекулярного переноса: кинематической вязкости  и коэффициента температуропроводности, а перенос импульса, связанный с величиной , определяется разностью скоростей, а перенос тепла, связанный с величиной а,— разностью температур. Следовательно, число Рr, явно содержащее лишь величины, определяющие физические свойства среды, в действительности характеризует отношение между полями скоростей и тем­ператур. Тогда зависимость Nu = f(Re, Pr) можно трактовать следующим образом: количество переносимого тепла (Nu) зависит от вида скоростного поля (Re) и его связи с полем температур (Рr). Для идеальных газов число Рr, однозначно определяемое числом атомов в молекуле и не зависящее от температуры и давления, приведено в табл.10.1.

Таблица 10.1