Математические модели геометрических объектов в трехмерном пространстве

Системы координат геометрических объектов в двухмерном пространстве

1. Декартова система координат

2. Полярная система координат

Системы координат в трехмерном измерении

1. Декартова система координат

2. Цилиндрическая система координат

3. Сферическая система координат

Геометрические объекты

Прямые

1 способ.

y = kx + b

k = tg α

2 способ.

Ax + By + D = 0

A = x_i+1 - x_i

B = y_i+1 - y_i

D = x_i+1 y_i - x_i y_i+1

3 способ.

4 способ.

Параметрический способ задания.

5 способ.

Матричный способ задания.

В матричных цифровых машинах.

6 способ.

В векторных цифровых машинах.

Дуги и окружности

1 способ.

Неявно.

2 способ.

Пример:

3 способ.

4 способ.

Кривые второго порядка

Общий вид уравнения второго порядка

Таким образом можно найти коэффициенты a, b, c, d, e.

Кривые второго порядка в параметрическом виде

Параметрические уравнения третьего порядка

Кривая Фергюсона

r – переменная, изменяющаяся от 0 до 1

n, p, m, q – вектора, определяющиеся из решения системы уравнения

Данное уравнение может быть представлено в матричном виде:

Универсальная степенная функция или кривая МАИ

l – максимальный размер

При значении f=0 и m=0 уравнение описывает уравнение окружности.

При значении f=0 и m=1 уравнение описывает уравнение параболы.

При значении f=1 и m=0 уравнение описывает уравнение прямой.

Интерполяция с помощью многочленов Лежандра

Пусть задан набор точек (x_1,y₁)(x₂,y₂)…(x_n,y_n), заданных на плоскости, причем x_i ≠ x_j при i≠j.

Для таких точек можно непосредственно написать формулу интерполяционного многочлена n-1 степени. Он будет иметь вид:

Или

Кусочно-квадратичный полином

Пусть на отрезке [a,b] задана сетка:

a ≤ x₁ < x₂ <…< x_n ≤ b

a ≤ y₁ < y₂ <…< y_n ≤ b

Аппроксимируем функцию, заданную сеткой, кусочно-квадратный полином вида:

В интервале

При этом накладывается условие:

1. неразрывна в узлах сетки

где

2. дифференцируема

3. значение производной в некотором узле = некоторому значению

Распишем подробнее накладываемое условие, тогда получим систему уравнений:

Методы аппроксимации сплайнами

«сплайн» - (фран. – «гибкая линейка»)

Введение

В общем виде кусочно-полиноминальный функции представляется

следующем образом:

Функция представляет собой многочлен со степенью не выше m.

Условие неразрывности в узлах задается вторым уравнением, у которого j является производной от функции p(x).

При условии когда n = m возникает максимальное количество ограничений, при этом существует особый случай когда n = m = 3 и этот случай получил впервые название (термин) сплайн.

Простым сплайном называется кусочно-полиноминальная функция, задаваемая системой уравнений при n = m.

Линейный, квадратичный, кубический сплайн отличается от кусочно-полиноминальной функции при n =1, 2, 3 соответственно.

Кубический сплайн

Пусть на отрезке [a,b] задана сетка:

a ≤ x₁ ≤…≤ x_n ≤ b

a ≤ y₁ ≤…≤ y_n ≤ b

Аппроксимируем на каждом отрезке I данной сетки кубический полином вида:

При этом необходимо чтобы выполнить следующее условие:

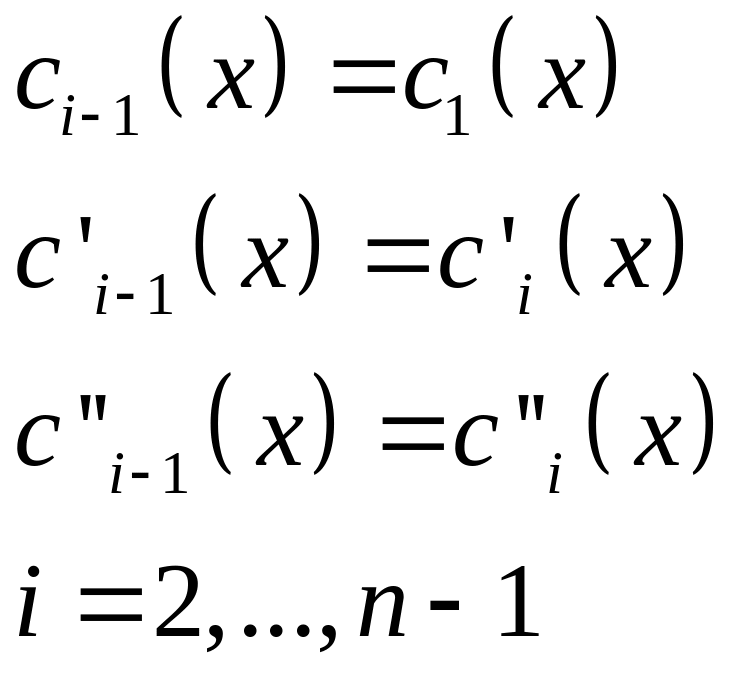
+2 условие, которое должно выполняться

Тогда в аналитическом виде можно записать:

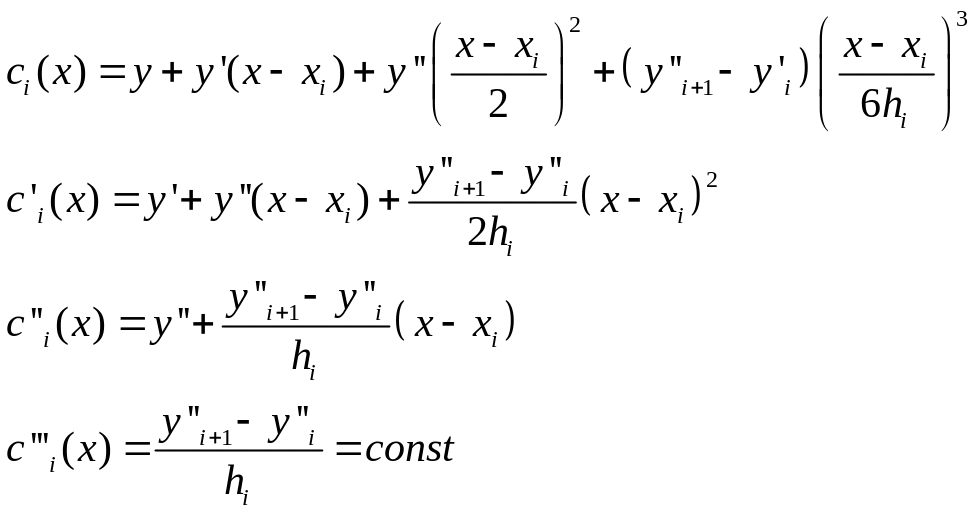
Вычисляется методом прогонки.

Многочлены Безье

Задаются в параметрической форме в следующем виде:

Пусть дан набор точек:

Данный набор точек называется ориентирами, тогда соответствующий многочлен Безье будет иметь вид:

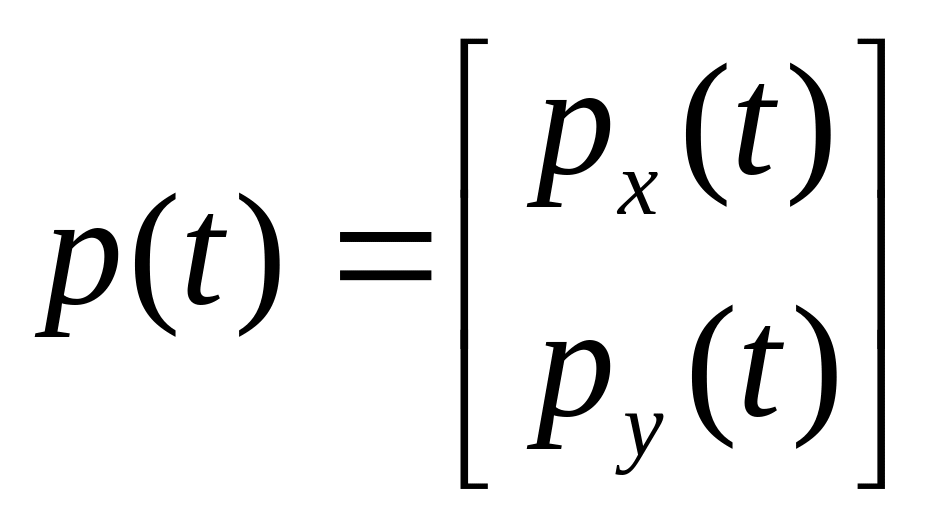
Тогда в матричном виде:

, где

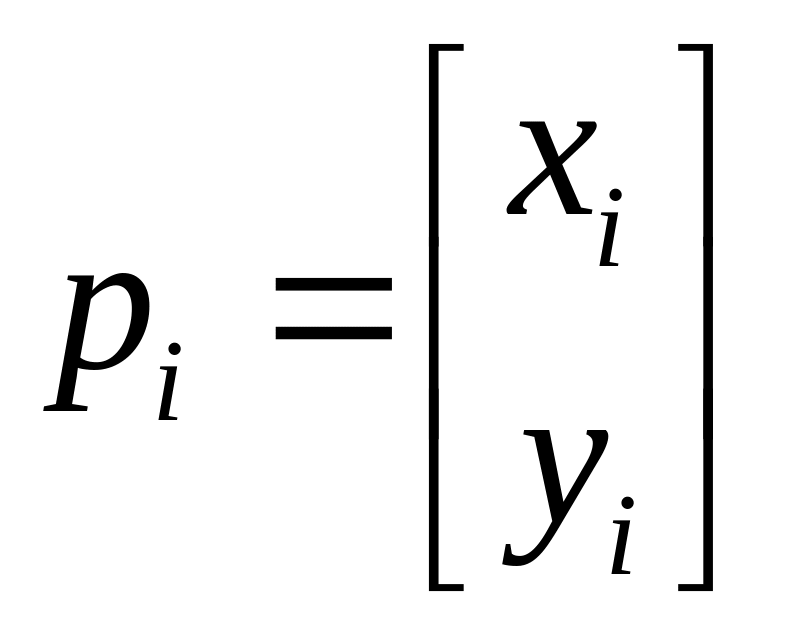
При числе m > 5 для нахождения членов Безье более эффективна схема Горнера.

Свойства кривых Безье:

1. Кривая, порождаемая многогранником Безье, обладает следующими свойством:

Любую дугу входящую в нее также можно породить с помощью многочленов Безье

2. При 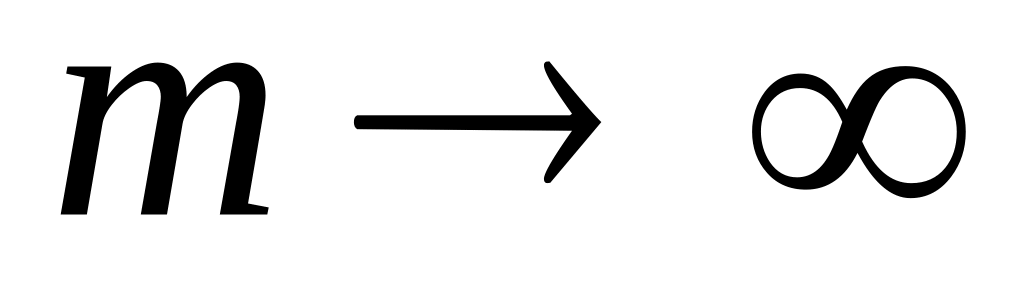кривая Безье к многограннику

Поверхности

Поверхность – непрерывное двухпараметрическое множество точек.

Поверхность считается заданной, если относительно любой точки пространства можно однозначно и сколь угодно точно решить вопрос о ее принадлежности к данной поверхности.

Поверхность может быть математически представлена в явном виде:

В неявном виде:

В параметрической форме:

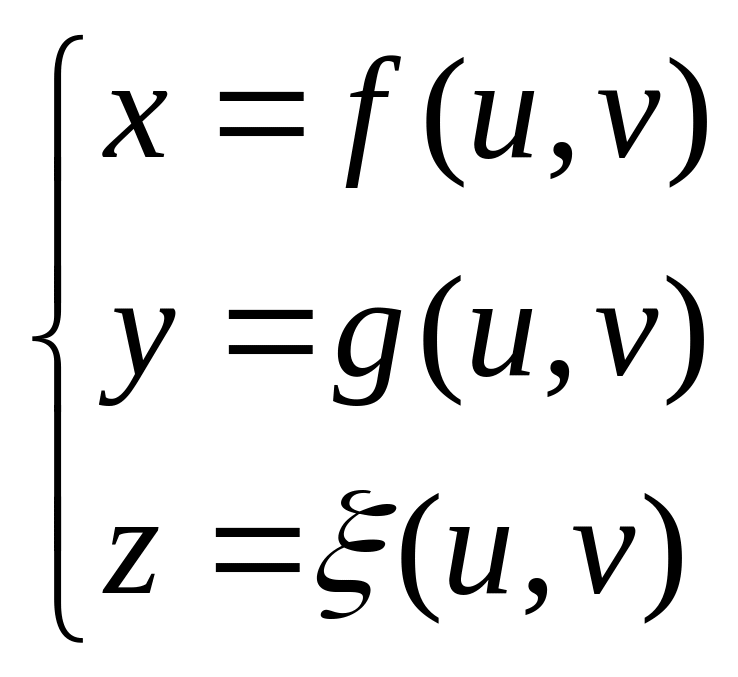
В векторной форме:

В матричной форме и других видах задания поверхности.

Поверхность получаемая полиномом Лагранжа

Простейший алгоритм построения поверхности, по исходному точечному базису заключается в обобщении метода Лагранжа для нахождения полинома, который будет интегрировать все заданные точки.

Этот полином имеет вид:

Недостаток данного способа:

При достаточно больших значениях p и q построенных таким образом поверхности, появляется нежелательная осцилляция, с которой борются уменьшением количества ячеек (точек), описывающим данный полином, это влечет за собой понижение степени полинома, описывающее данную поверхность.

Уравнение полиноминальной поверхности в форме Безье

Уравнение полиноминальной поверхности в форме Безье имеет вид:

r_ij – вершина характерного многогранника

m – число вершин по направлению движения v

n - число вершин по направлению движения u

i – текущая вершина по направлению u

j – текущая вершина по направлению v.