Дифференциальное исчисление функций одной переменной

1)Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,

Прямо из определения следует, что график касательной прямой проходит через точку . Угол между касательной к кривой и осью Ох удовлетворяет уравнению

где обозначает тангенс, а — коэффициент наклона касательной. Производная в точке равна угловому коэффициенту касательной к графику функции в этой точке.

Пусть — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

2) Найти производную от функции, заданной неявно

1) На первом этапе навешиваем штрихи на обе части:

2) Используем правила линейности производной):

3) Непосредственное дифференцирование.

. В параметрической форме функция задается двумя уравнениями: . Переменная называется параметром и может принимать значения от «минус бесконечности» до «плюс бесконечности».

Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения , область значений этой функции , тогда на интервале определена непрерывная строго монотонная функция с областью значений , которая является обратной для . Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает. Функции f и g называют взаимно обратными.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.

3)Функция =f(x) дифференцируема в т. , если ее приращение можно представить в виде ∆y=A*∆x+α(∆x)*∆x,(1) где α(∆х)-б.м.ф. ∆→0.Т1: Для того чтобы функция была дифференцируема в т. необходимо и достаточно, что бы в этой точке существовала производная этой функции. Т2: Если функция дифференцируема в , то она непрерывна в этой точке. обратное не верно.

Дифференциалом функции наз-ся главная, линейная относительно ∆х часть приращения функции в формуле (1),т.е. приращение аргумента dx=∆x. y(x)≈y( )+y’( )(x- -формула использования дифференциалом для приближенных значений.

4) . Теорема Ферма

Пусть функция определена и непрерывна на интер-е (а,в),и в точке принимает наибольшее или наимменьшее значение, принадлежит (а,в), тогда f’(x)=0.

Геометрическое истолкование теоремы вытекает из геометрического смысла производной: касательная к графику функции в точке с абсциссой параллельна оси . f’( )=k* =0.

Теорема Ролля

Пусть функция непрерывна на отрезке (а,в) и дифференциируема в интервале (а,в), кроме того f(в)=f(а), тогда существует С принадлежащая (а,в) и f’(C)=0

Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.

Теорема Лагранжа

Пусть функция непрерывна на отрезке (а,в) и дифференциируема в интервале (а,в), тогда существует С принадлежащая (а,в): f’(C)= .

Замечание: Часто эту теорему называют формулой конечных приращений и используют в виде: f(B)-f(a)=f’(c)*(B-a).

Геометрическое истолкование теоремы Лагранжа

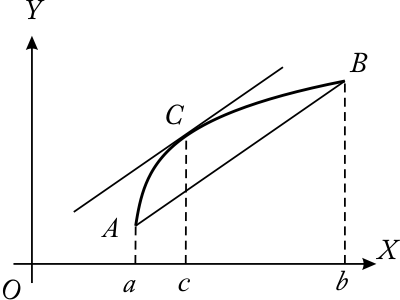
5) Пусть в интервале (a, b) задана функция f(x) и в каждой точке x  (a, b) существует производная f '(x). Таким образом в интервале (a, b) задана функция y = f '(x) .

Если первая производная функция y = f '(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f(x).

Вторая производная обозначается символами f ''(x) или .

Производной n–го порядка функции f(x), называется производная от производной функции f(x) (n − 1)–го порядка.

Замечание. Если речь идет о производной n–го порядка ( n = 2, 3, … ) в фиксированной точке x₀, то для существования f⁽ⁿ⁾ (x₀) необходимо существование f^{(n − 1)} (x) не только в точке x₀, но и в некоторой ее окрестности. f’’( )= * ( )

Функция, имеющая в точке производную n–го порядка, называется n раз дифференцируемой в этой точке.

Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.

Формулы для производных n–го порядка суммы и произведения функций :

производная n–го порядка произведения определяется формулой Лейбница

Если функции u(x) и v(x) n раз дифференцируемы на некотором промежутке, то производная n–го порядка суммы определяется формулой

( u + v )(n) = u(n) + v(n) , Пусть в интервале (a, b) задана дважды дифференцируемая функция y = f(x), где x — независимая переменная. Фиксируем приращение dx = Δx независимой переменной x, т.е. будем считать первый дифференциал dy = f'(x) dx (1) функцией только переменной x.

Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f(x) в точке x и обозначается d² f(x). формулу для вычисления второго дифференциала

d2 f(x) = f ''(x) dx2 .

(2)

Дифференциалом n–го порядка называется дифференциал от дифференциала (n − 1)–го порядка

dn f(x) = d (d(n − 1) f(x)).