3) Определение функции

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Основные свойства функции. 1. Четность и нечетность

2.Периодичность

3. Монотонность (возрастание, убывание)

4. Экстремумы

5. Нули функции

4) Точку (действительное число) a называют пределом (значений) функции f(x) x  X, в точке х₀ если для любой сходящейся к последовательности аргумент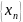 соответствующая последовательность значений. сходится к А. 

Свойства предела функции.

1. Если функция f заданная на множестве Х имеет конечный предел в точке х₀, тогда найдется окрестность U этой точки, такая, что функция fбудет ограничена на пересечении U и Х.

2. Если функция f заданная на множестве Х имеет конечный и не равный 0 предел а в точке х₀, тогда найдется окрестность U этой точки и положительное число c, такие, что при a > 0 на пересечении верно f(x) > c ; а при a < 0 на пересечении U и Х верно f(x) < – c.

3. Если f(x) = C для всех x, тогда предел этой функции равен C. Если f(x)  C для всех x, тогда предел этой функции больше или равен C.

4. Если g(x)  f(x)  h(x) и пределы функций g и <h в точке х₀ равны между собой и равны a, то предел f(x) в этой точке также равен a.

5. Если у функцийg(x) и f(x) существуют пределы, равные a и b соответственно, тогда выполняются следующие арифметические свойства пределов :

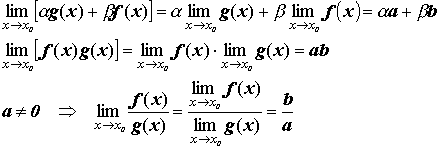
Именуемые пределом линейной комбинации (суммы), пределом произведения и пределом отношения.

6. Для вычисления предела суперпозиции функций g(f(x)) нужно вычислить предел   , а затем нужно вычислить предел g(x) при условии, что x  a.

6) Функции f(x),   непрерывна в точке  , если

Теорема. Функция f(x),   непрерывна в точке   тогда и только тогда, когда

Пусть x₀ - точка разрыва функции f(x),   , тогда имеют место следующие типы разрывов.

1. Устранимый разрыв первого рода: если f(x₀ - x) = f(x₀ + x) ≠ f(x₀) либо f(x₀ - 0) = f(x₀ + 0) , а f(x0) не существует

2. Неустранимый разрыв первого рода: если f(x₀ - 0) ≠ f(x₀ + 0) . Разрыв второго рода: если хотя бы один из пределов f(x₀ - 0) или f(x₀ + 0) не существует или бесконечен

Свойства непрерывных функций на отрезке:

1)Если функция непрерывна в каждой точке отрезка АВ, то она непрерывна на отрезке АВ.

2)Если функция непрерывна в т. , то можно менять предел функции и саму функцию местами.