Каноническое уравнение:

8.Поверхности второго прядка: классификация и виды, построение.

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

 (1).

Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c - сжатым. В случае, когда a=b=c, эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), - двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), - гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

10.Полярная система координат: формулы перехода, построение точек и линий в полярной системе координат.

Полярная система координат – система плоских координат образованная направленным прямым лучом OX, называющимся полярной осью. Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат - точка O - называется полюсом системы.

Если полярную и декартову прямоугольную системы совместить так, чтобы начала их координат совпадали, а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы, то независимо от расположения точки B на плоскости получим формулы перехода от полярных координат r, a к декартовым x, y:

x = r cos a; y = r sin a (1)

и от декартовых к полярным:

 (2)

Положение любой точки в полярной системе определяется двумя координатами: радиусом-вектором r (или полярным расстоянием S) – расстоянием от полюса до точки, и полярным углом b при точке O, образованным осью OX и радиусом вектором точки и отсчитываемым от оси OX по ходу часовой стрелки.

Дифференцирование функций одной переменной

2)Если любые натуральные числа 1,2,3… ставятся в соответствие действительным числам а1,а2,а3…, то говорят что это числовая последовательность . Числовые последовательности бесконечны.

Числовая последовательность, не ограничена , если для любого n принадлежащего Nвыполняется неравенство , и наоборот наз-ся ограниченной если она ограничена сверху и снизу.

Последовательность наз-ся бесконечно большой, если для любого А>0 выполняется неравенство:

Последовательность наз-ся бесконечно малая, если для любого Ԑ>0, n>N выполняется неравенство: .

Свойства:1)если последовательность -б.б., то послед-ть -б.м.; 2) если - б.м. ,то –б.б. 3)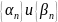 -б.м. то -б.м., 4) -б.м, 5) на ограниче.произв.-б.м.. Следствие: Произведение б.м. на константу : -б.м.

Число. А наз-ся пределом ,если для любого Ԑ>0, начиная с некоторого n>N выполняется неравенство:

Если последовательность имеет конечный предел, то она сходящаяся, в противном случае- расходящаяся.

Суммой рядов наз-ся предел последовательности его частичных сумм.

Если последовательность частичных сумм ряда сходящаяся, то ряд сходится, и наоборот.