
- •Дискретная математика
- •Линейная алгебра и геометрия
- •3) Совокупность уравнений
- •Формула координаты середины отрезка
- •7.Прямая и плоскость в пространстве: основные уравнения прямой и плоскости, взаимное расположение двух прямых, двух плоскостей, прямой и плоскорсти.
- •Каноническое уравнение:
- •8.Поверхности второго прядка: классификация и виды, построение.
- •Дифференцирование функций одной переменной
- •3) Определение функции
- •Дифференциальное исчисление функций одной переменной
- •Формула для вычисления дифференциала n–го порядка
- •8) Формула тейлора
- •Численные методы
- •1) Абсолютной погрешностью или, короче, погрешностью приближённого числа называется разность между этим числом и его точным значением (при этом из большего числа вычитается меньшее).
- •3) Полином Лагранжа
Формула координаты середины отрезка
![]()
![]()
7.Прямая и плоскость в пространстве: основные уравнения прямой и плоскости, взаимное расположение двух прямых, двух плоскостей, прямой и плоскорсти.
Плоскость и прямая в пространстве |
Назовем
нормалью к плоскости вектор,
перпендикулярный к этой плоскости.
Обозначают нормаль
Определение. Уравнением
поверхности в пространстве Пусть
точки Укажем теперь основные уравнения плоскостей: 1) 2) 3) 4) угол
между двумя плоскостями,
который равен углу между нормалями к
плоскостям ( или дополняет этот
последний до
Расстояние
от точки
Основные уравнения прямых в пространстве: 1) 2) 3) Взаимное расположение двух прямых в пространстве определяется расположением их направляющих векторов. в)
угол между прямыми В
заключение темы рассмотрим взаимное
расположение прямой и плоскости в
пространстве. Ясно, что прямая Прямая
перпендикулярна плоскости при
условии
Угол между прямой и плоскостью находят по формуле
8.Кривые второго порядка: эллипс, гипербола, парабола: определение, канонические уравнения, свойства, способ построения. Кривой второго порядка называется линия на плоскости, которая в некоторой системе координат определяется уравнением
где
А, В, С, D, E, F - вещественные коэффициенты,
причем
Если Если Если В процессе исследования кривых 2-го порядка, уравнение которых записано в общем виде, полезна "процедура выделения полного квадрата". Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами. Каноническое уравнение:
Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы. Если 2c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение a2 + b2 = c2. При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид x2 - y2 = a2. Фокусы гиперболы лежат на ее действительной оси. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.
Асимптоты гиперболы - две прямые, определяемые уравнениями
Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами). Каноническое уравнение:
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение a2 - b2 = c2. Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси. |
Параболой называется множество всех точек плоскости, равноудаленных от точки, называемой фокусом, и от прямой, называемой директрисой.


 –
уравнение плоскости, проходящей через
три заданные точки
–
уравнение плоскости, проходящей через
три заданные точки 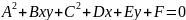

 ,
то эллипс;
,
то эллипс; ,
то гипербола;
,
то гипербола; ,
то парабола.
,
то парабола.