3) Полином Лагранжа

Решение ищем в виде  , где l_i(z) – базисные полиномы N–й степени, для которых выполняется условие:  . Убедимся в том, что если такие полиномы построены, то L_N(x) будет удовлетворять условиям интерполяции:

.

Каким образом построить базисные полиномы? Определим

, i=0, 1,..., N.

Легко понять, что

, и т.д.

Функция l_i(z) является полиномом N–й степени от z и для нее выполняются условия "базисности":

=0, i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.

.

Таким образом, нам удалось решить задачу о построении интерполирующего полинома N– й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы:  . Погрешность этой формулы можно оценить, если исходная функция g(x) имеет производные до N+1 порядка:

.

Из этой формулы следует, что погрешность метода зависит от свойств функции g(x), а также от расположения узлов интерполяции и точки z. Как показывают расчетные эксперименты,полином Лагранжа имеет малую погрешность при небольших значениях N<20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).

4) . Метод половинного деления известен также как метод бисекции. В данном методе интервал делится ровно пополам.

Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции - и это весьма важное свойство. Недостатком метода является то же самое - метод никогда не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем случае.

Метод половинного деления:

1. Один из простых способов поиска корней функции одного аргумента.

2. Применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимумили конкретное число).

Метод половинного деления как метод поиска корней функции

Изложение метода

Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.

Будем считать, что корень   функции   отделён на отрезке  . Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью  .

Пусть функция   непрерывна на отрезке  ,

 и   - единственный корень уравнения  .

(Мы не рассматриваем случай, когда корней на отрезке   несколько, то есть более одного. В качестве   можно взять и другое достаточно малое положительное число, например,  .)

Поделим отрезок   пополам. Получим точку   и два отрезка  .

• Если  , то корень   найден ( ).

• Если нет, то из двух полученных отрезков 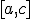  и   надо выбрать один   такой, что 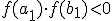 , то есть

  • , если   или

  • , если  .

Новый отрезок   делим пополам. Получаем середину этого отрезка   и так далее.

Для того, чтобы найти приближённое значение корня с точностью до  , необходимо остановить процесс половинного деления на таком шаге  , на котором   и вычислить  . Тогда можно взять  .

Метод касательных.

1. Задается начальное приближение  .

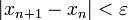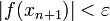2. Пока не выполнено условие остановки, в качестве которого можно взять   или   (то есть погрешность в нужных пределах), вычисляют новое приближение:  .