8. Программирование задачи численного решения алгебраических уравнений

Уточнение корней алгебраических уравнений.

f(x)=0

Для решения уравнений используются численные методы (ЧМ). Они позволяют решить задачу при конкретных числовых данных. Полученное решение, как правило, является приближенным, но при решении задачи контролируют точность результата.

ЧМ используются:

1. Интегрирование;

2. Решение алгебраических уравнений;

3. Решение дифференциальных уравнений и систем;

4. Решение интегральных уравнений.

ЧМ являются более универсальными, чем аналитические.

Численное интегрирование

Данная задача решается путем вычисления конечных сумм.

x _i y_i=f(x_i)

Численное решение алгебраических уравнений

Состоит из 2-х этапов:

1. Отделение корней

2. Уточнение корня

1.ищется интервал (a,b), внутри которого1-н единственный корень исходного уравнения.

2.в пределах найденного интервала (a,b) корень уточняется, т.е. находится с заданной погрешностью .

Для уточнения корней используются различные различные методы и алгоритмы:

1. Метод половинного деления

2. Метод касательной (м. Ньютона)

3. Метод хорд (м. пропорциональных частей)

4. Метод итераций

5. Комбинирующие методы

Метод половинного деления

- условие выхода из цикла

Данный метод является универсальным и медленно действующим.

Метод касательной

Метод хорд

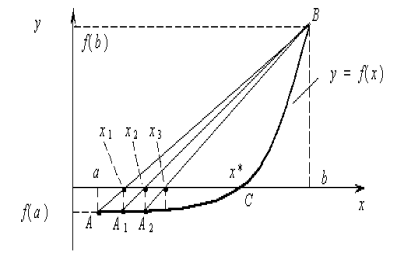
Метод итераций

9. Алгоритмы вычисления конечных сумм и произведений

Очень часто встречаются задачи, связанные с вычислением суммы конечного числа слагаемых:

S = f₁ + f₂ + … + f_n

Для обозначения этой суммы целесообразно использовать знак суммы . Тогда эту сумму можно будет записать в виде:

Здесь i - индекс суммирования, который меняется от 1 (начальное значение) до n (конечное значение) с шагом 1, f_i - выражение общего члена. Из выражения f_i при значении i = 1 получится первое слагаемое в сумме, при i = 2 - второе... и, наконец, при i = n последнее слагаемое.

Для указанной суммы вычисления можно организовать в виде циклического алгоритма, когда после каждого шага цикла номер слагаемого увеличивается на единицу, а сумма изменяется на величину i - ого слагаемого.

Пример 3. Cоставьте программу вычисления суммы.

Указание: знаки, начиная со второго слагаемого, в сумме чередуются  (+, - , +, - и т.д.). Закон чередования знаков (+, - или -, + ) можно описать с помощью дополнительного множителя (-1)ⁱ либо (-1)ⁱ⁺¹. Первое слагаемое нельзя описать с помощью общей формулы, справедливой для всех членов, поэтому необходимо вынести его за знак суммы.

Имеем S = 1+  

REM Вычисление суммы

INPUT “Введите значение x = ”; x

 S = 1

 FOR I =1 TO 100

 S = S + (-1)^(I+1)*X^I/I

 NEXT I

 PRINT “S = ”; S

 END 

Для вычисления произведения конечного числа сомножителей воспользуемся символом П

 

  При такой записи целочисленный индекс i меняется от 1 до числа n с шагом 1, где n -  количество сомножителей в произведении. При i = 1 получаем первый сомножитель, при i = 2 — второй и т.д., при i = n —  n - ый сомножитель. Как и сумму,  произведение можно вычислить с помощью циклического процесса. 

 

Составьте программу вычисления произведения.

 

   Имеем

 

  INPUT  “Введите число х=”; х

   P = 1

   FOR  I = 1 TO 7

   Т=х2^I

   P= P*T/(T+1)

   NEXT I

   PRINT “P= ”; P

   END.