6.3.4. Картометрические приемы

Предельная точность масштаба карты – отрезок на местности, соответствующий 0,1 мм в масштабе данной карты. При масштабе карты 1:100 000 предельная точность составит 10 м, при масштабе 1:10 000 она будет равна 1 м.

Рис. 196. Измерение извилистой линии циркулем-измерителем

Рис. 197. Поперечный масштаб

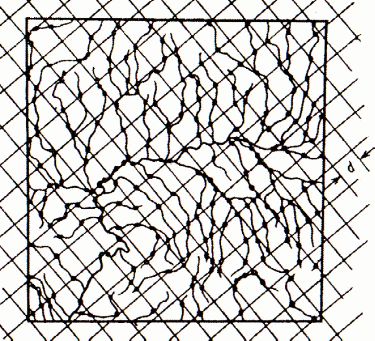Рис. 198. Палетка

Измерение длин извилистых линий. На картах крупных масштабов длины извилистых линий измеряют с предельной точностью с помощью циркуля-измерителя и поперечного масштаба.

Для измерения длин извилистых линий используют циркуль-измеритель с малым раствором игл – (m = 2-4 мм). Тогда длина извилистой линии (L) на карте будет равняться произведению раствора циркуля и числа отложений (шагов) циркуля n: L = m·n.

Однако даже измерения с помощью измерителя с малым раствором не дают истинных длин, так как в результате генерализации извилистые линии на картах бывают укорочены по сравнению с реальными.

При работе с картами часто появляется необходимость подсчитать суммарную длину извилистых линий на некотором участке, например длину эрозионной сети в речном бассейне и т.п. В таких случаях обращаются к вероятностным приемам с использованием палеток. На измеряемую сеть извилистых линий произвольно накладывают прозрачную палетку в виде сетки квадратов со стороной d = 1–5 мм и подсчитывают число пересечений m извилистых линий с сеткой. Суммарная длина извилистых линий Σl определяется по формуле: Σl = π d m /4.

Относительная погрешность измерения при этом составляет 3–5 %, но в особо неблагоприятных случаях может достигать 10 %. Если нужно получить результат с большей точностью, то палетку можно повернуть, вновь подсчитать число пересечений и взять среднее. Тогда формула примет вид: Σl = π d m /4N, где N – число наложений палетки. Точность вероятностных определений зависит от параметра палетки (d), числа наложений (N) и от плотности самих извилистых линий, их взаимной ориентации. Точность наименьшая, если сеть извилистых линий редкая, а сами линии примерно параллельны друг другу. При плотности сети извилистых линий 1–2 см /см² погрешность определения их суммарной длины палеткой с шириной клеток от 2 до 4 мм составляет около 6–8%, а при густой сети (10–12 см / см²) относительная погрешность близка к 2,5%.

Измерения площадей по картам осуществляют с помощью планиметров, методом взвешивания и палетками разных конструкций.

Планиметр – специальный прибор для определения по карте или плану площади участка местности. Использование планиметра удобно при измерении крупных контуров порядка 10–15 см². В этих случаях относительная погрешность измерений составляет около 1%. Однако при измерении мелких контуров точность измерения площадей планиметром невысока.

При способе взвешивания контуры, площадь которых требуется определить, переносят на кальку, а затем аккуратно вырезают и взвешивают на аналитических весах с точностью до 0,0001 г. Из этой же кальки вырезают и взвешивают эталонный участок, площадь которого известна, что позволяет определить цену единицы веса. Средние относительные погрешности данного способа составляют 1,6–2,2 %. Способ взвешивания удобен при определении суммарной площади множества мелких ареалов (например, при определении общей площади небольших сельхозугодий, почвенных выделов и т.п.).

Для измерения площадей применяются разного вида палетки:

• квадратная палетка: P = a²n, где a – сторона квадрата в масштабе карты, n – число квадратов, попавших в пределы измеряемого контура;

• палетка, состоящая из системы параллельных линий: P = d Σl, где d – расстояние между линиями палетки, Σl – суммарная длина отрезков, отсекаемых контуром измеряемого участка;

• точечная квадратная палетка: P = a²n, где а – расстояние между точками; n – число точек, попавших в пределы контура;

• точечная гексагональная палетка: P = (а²n√3) /2, где а – расстояние между точками; n – число точек, попавших в пределы контура.

Точность определения площадей с помощью палеток не ниже, чем точность планиметрирования и взвешивания, а для малых контуров – даже выше. При использовании достаточно мелких палеток (сторона квадрата или расстояние между точками а = 1,5–2 мм, расстояние между линиями палетки d = 2–4 мм) относительные погрешности составляют около 1,5–3 %. При прочих равных условиях наибольшую точность измерения площадей обеспечивают сетки параллельных линий, затем гексагональные и квадратные палетки.

Измерение объемов. Если объект изображен на карте в изолиниях, то его объем V можно представить как сумму объемов отдельных слоев v_n, заключенных между плоскостями сечения:

V = v₁+ v₂+ …+ v_n = (p₁+ p₂ /2)h₁ + (p₂ + p₃ /2)h₂ + …+ (p_n + p_n+1 /2)h_n + 1/3 p_n Δh, где p_n  и p_n+1 – площади нижней и верхней плоскостей, ограничивающих слой; h_n – высота слоя; 1/3p_n Δh – объем вершины объекта, имеющей превышение Δh над самой верхней плоскостью сечения.

Изоколы - линии, соединяющие точки с одинаковыми значениями искажений площадей и углов.

Измерения углов и направлений на картах, не имеющих искажений углов, не представляют сложности и выполняются с помощью геодезического транспортира с точностью до 15%. В равновеликих и равнопромежуточных проекциях способы измерения углов и направлений сложны и индивидуальны для каждой проекции. Для ряда проекций имеются карты с изоколами углов, составлены специальные таблицы, позволяющие вычислить ориентировочные углы по координатам начальной и конечной точек направления, минуя непосредственные измерения. Однако если необходимо проводить многочисленные замеры углов, а искажениями нельзя пренебречь, то пользование этими таблицами отнимает много времени, и целесообразно перенести измерения на другую карту, где искажения отсутствуют.