39. Проектный и проверочный расчеты на контактную прочность цилиндрической косозубой передачи.

Работоспособность ряда деталей машин (зубчатых колес, подшипников качения и др.) определяется контактной прочностью, т. е. прочностью их рабочих (контактирующих) поверхностей.

Проектный расчет. Аналогично расчету прямозубой передачи межосевое расстояние для стальной косозубой парs .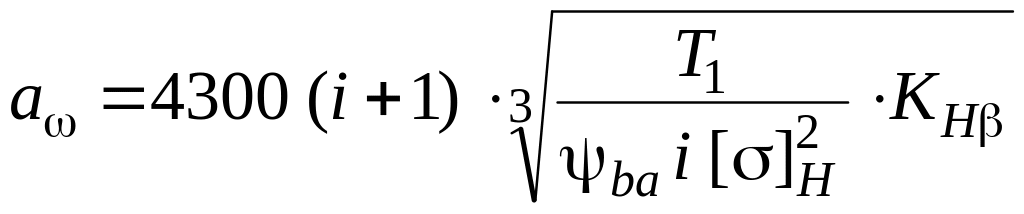

Проверочный расчет. Аналогично расчету прямозубой передачи контактные напряжения в поверхностном слое косых зубьев , где дополнительно по ГОСТ 21354—75:  коэффициент, учитывающий форму сопряженных поверхностей зубьев. Среднее значение ; Па^1/2  для стальных колес;  коэффициент, учитывающий перекрытие зубьев. Среднее значение . Следовательно, где  коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых колес при м/с для 68-й степеней точности, ;  коэффициент неравномерности нагрузки по ширине венца;  коэффициент динамической нагрузки. Для косозубых передач рекомендуется при любой твердости зубьев и м/с;  при твердости зубьев  НВ350 и м/с;  при твердости зубьев > HВ350 и м/с.

40. Коническая прямозубая передача. Передаточное отношение и передаточное число. Основные геометрические соотношения.

Конические зубчатые колеса применяют в передачах, когда оси валов пересекаются под углом

Наибольшее распространение имеют передачи с углом, ∑ = 90o ,.Конические колеса бывают с прямыми (а), круговыми (б) и редко с шевронными зубьями.

Конические прямозубые передачи имеют начальный линейный, а передачи с круговыми зубьями – точечный контакт в зацеплении.Общее передаточное отношение для зубчатых передач определится по зависимости: . Передаточное отношение: .Существует понятие передаточного числа: .

Основные геометрические соотношения

Параметры	Формулы
1	Число зубьев	Z2
2	Модуль нормальный, мм	mn=m
3	Шаг нормальный, мм
4	Угол исходного контура
5	Угол наклона зубьев
6	Торцовый модуль, мм
7	Торцовый шаг, мм
9	Коэффициент ножки зуба	С rn > 1
10	Диаметр делительной окружности, мм	d = Z * mt
16	Межосевое расстояние, мм	A = 0,5 (d1 + d2)

42. Проектный и проверочный расчеты на изгибную прочность конической прямозубой передачи.

Расчет конической передачи на прочность основан на допущении, что несущая способность зубьев конического колеса будет такой же, как и у эквивалентного цилиндрического, с той же длиной зуба b и профилем, соответствующим среднему дополнительному конусу (среднему сечению зубьев). Однако практика эксплуатации показала, что при одинаковой степени нагруженности конические передачи выходят из строя быстрее цилиндрических. Поэтому при расчете вводят коэффициент понижения допускаемой нагрузки конической зубчатой передачи по сравнению с эквивалентной цилиндрической. Этот коэффициент равен 0,85.

Проектный расчет. Аналогично расчету цилиндрической прямо­зубой передачи средний модуль зубьев где дополнительно:  коэффициент неравномерности нагрузки;  коэффициент ширины венца колеса по отношению к среднему делительному диаметру;  коэффициент формы зуба эквивалентного колеса. Выбирают по .В формулу (17.43) подставляют меньшее из двух отношений для шестерни и колеса.Проверочный расчет. Аналогично расчету цилиндрической прямозубой передачи расчетные напряжения изгиба в зубьях конических колес и условие их прочности выражаются формулами: ; , где  коэффициент динамической нагрузки.

43. Проектный и проверочный расчеты на контактную прочность конической прямозубой передачи.

Проверочный расчет выполнятся по формуле, которая записывается через параметры эквивалентного прямозубого цилиндрического колеса: . Заменив в этой формуле и , получим формулу проверочного расчета для стальных конических прямозубых колес . Заменив в формуле , , получим формулу проектного расчета стальных конических прямозубых передач .

48. Червячная передача. Достоинства, недостатки и применение. Классификация. Нарезание червяков и червячных колес.

Червячные передачи применяют для передачи вращательного движения, между валами, у которых угол скрещивания осей обычно составляет .

Червячные передачи широко применяют в станках, подъемно-транспортных машинах, троллейбусах и т. д.

Червячные передачи рекомендуется применять в качестве быстроходной ступени и в приводах периодического действия во избежание их перегрева.

В большинстве случаев ведущим является червяк

Классификация червячных передач

1. В зависимости от формы внешней поверхности червяка:

а) с цилиндрическим червяком;

б) с глобоидным червяком.

2. В зависимости от направления линии витка:

а) с левым направлением;

б) с правым направлением.

3. В зависимости от числа витков (заходов резьбы)

а) одновитковые червяки;

б) многовитковые червяки.

4. В зависимости от расположения червяка относительно колеса:

а) с нижним расположением червяка;

б) с боковым;

в) с верхним.

5. В зависимости от формы винтовой поверхности цилиндрического червяка:

а) с архимедовым червяком;

б) с конволютным;

в) с эвольвентным.

Нарезание

Архимедовы червяки подобны ходовым винтам с трапеце­идальной резьбой. Основными способами их изготовления являются:

1)   нарезание резцом на токарно-винторезном станке (рис. 15.4; этот способ точный, но малопроизводительный);

2)   нарезание модульной фрезой на резьбофрезерном стан­ке (способ более производительный).

Работоспособность червячной передачи зависит от твердости и шероховатости винтовой поверхности резьбы червяка, поэтому после нарезания резьбы и термообработки червяки часто шлифу­ют, а в отдельных случаях полируют. Архимедовы червяки приме­няют и без шлифовки резьбы, так как для шлифовки их требуются круги фасонного профиля, что затрудняет обработку. Эвольвент- ные червяки можно шлифовать плоской стороной круга на специ­альных червячно-шлифовальных станках.

Червячные колеса чаще всего нарезают червячными фрезами (рис. 15.5), причем червячная фреза должна представ­лять копию червяка, с которым будет зацепляться червячное колесо. При нарезании заготовка колеса и фреза совершают такое же взаимное движение, какое будут иметь червяк и червяч­ное колесо при работе.

49. Основные геометрические соотношения в червячной паре. Червячные передачи со смещением.