26. Правило «трех сигма».

В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x. Для любой случайной величины x с математическим ожиданием mx и квадратичным отклонением σx вероятность отклонения x от mx, больших по абсолютной величине k·σx, k > 0, не превосходит 1/k2 (неравенство Чебышева). В случае нормального распределения указанная вероятность при k = 3 равна 0.0027. В практических задачах, приводящих к нормальному распределению, чаще всего пренебрегают возможностью отклонения от среднего, большего 3·σx.

27. закону равномерной плотности. [5

Приведем пример случайной величины, распределенной с равномерной вероятностью.

Поезда метрополитена идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т,в течение которого ему придется ждать поезда, представляет собой СВ, распределенную с равномерной плотностью на участке (0, 2) минут.

Рассмотрим СВ X, подчиненную закону равномерной плотности на участке от а до в (см. рисунок 5.6). Плотность этой величины f (x) постоянна и равна с на отрезке (а, в); вне этого отрезка она равна нулю:

 (5.29)

Так как площадь, ограниченная кривой распределения, равна единице: c (в-а)=1. Отсюда получаем:c=1/(в-а).

Поэтому плотность распределения f (x) примет вид:

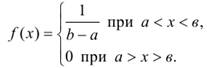 (5.30)

Рисунок 5.6 — График равномерной плотности распределения

Эта формула и выражает закон равномерного распределения вероятностей (закон равномерной плотности) на участке (а, в).

Напишем выражение для функции распределения F (x), которая выражается площадью, ограниченной кривой распределения и осью абсциссы, лежащей левее точки х (рисунок 5.6):

 (5.31)

График функции распределения F (x) приведен на рисунке 5.7.

Основные числовые характеристики СВ X на участке от  а до в:

— математическое ожидание величины X:

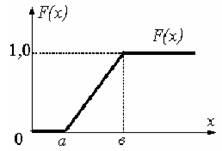
Рисунок 5.7 — Функция распределения

— дисперсия величины X:

— среднее квадратическое отклонение:

Найдем вероятность попадания СВ X распределенной по закону равномерной плотности, на участок (х1, х2), представляющий собой часть участка (а, в) (рисунок 5.8).

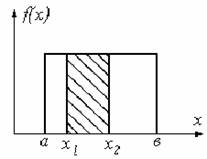
Рисунок 5.8 — Вероятность попадания величины X на участок(х1, х2)

Геометрически, как это видно из рисунка 5.8, вероятность представляет собой заштрихованную площадь и равна:

28. Закон Пуассона.

Рассмотрим прерывную случайную величину  , которая может принимать только целые, неотрицательные значения:

,

причем последовательность этих значений теоретически не ограничена.

Говорят, что случайная величина   распределена по закону Пуассона, если вероятность того, что она примет определенное значение  , выражается формулой

  ,               (5.9.1)

где а – некоторая положительная величина, называемая параметром закона Пуассона.

Ряд распределения случайной величины  , распределенной по закону Пуассона, имеет вид:

Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (5.9.1), может представлять собой ряд распределения, т.е. что сумма всех вероятностей   равна единице. Имеем:

Но

,

откуда

.

На рис. 5.9.1 показаны многоугольники распределения случайной величины  , распределенной по закону Пуассона, соответствующие различным значениям параметра  . В таблице 8 приложения приведены значения   для различных  .

Рис. 5.9.1.

Определим основные характеристики – математическое ожидание и дисперсию – случайной величины  , распределенной по закону Пуассона. По определению математического ожидания

.

Первый член суммы (соответствующий  ) равен нулю, следовательно, суммирование можно начать с  :

Обозначим  ; тогда

.