1. Классическое определение вероятности: Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:

,

где m_A- число исходов, благоприятствующих появлению события А.

Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей.

1. Суммой (объединением) двух событий А и В называется новое событие А+В, заключающееся в проявлении хотя бы одного из этих событий.

2. Произведением (пересечением) двух событий А и В называется новое событие АВ, заключающееся в одновременном проявлении обоих событий. А*В=АВ, АА=А, АВА=АВ.

3. Событие А влечет за собой появление события В, если в результате наступления события А всякий раз наступает событие В. АÌВ

А=В: АÌВ, ВÌА

2. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области   в так, что вероятность попадания точки в любую часть   не зависит от формы или расположения   внутри  , а зависит лишь от меры области   (и, следовательно, пропорциональна этой мере):

«Мерой» мы пока будем называть длину, площадь, объем и т.д.

Если для точки, брошенной в область  , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области  .

Пример:Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку   равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку   не является невозможным событием  —  это один из элементарных исходов эксперимента.

3. Теорема сложения вероятностей.

Вероятность суммы несовместных событий равна сумме вероятностей событий:

Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +…

Следствие. Если события A₁+A₂+…+A_n - полная группа событий, то сумма их вероятностей равна 1.

P(A+ ) = P(A) + P( ) = 1

Вероятность наступления двух совместных событий равна:

Р(А+В) = Р(А) + Р(В) - Р(АВ)

4. Теорема умножения вероятностей. Условные вероятности.

Опыт повторяется n раз, m_B раз наступает событие В, m_АВ раз наряду с событием В наступает событие А.

hn(B) = hn(AB) =

Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:

- условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.

5. Формула полной вероятности.

Вероятность события В, которое может произойти совместно только с одним из событий Н₁, Н₂, …Н_n , образующих полную группу событий, вычисляется по формуле:

События А₁, А₂, …А_n называют гипотезами.

6. Теорема гипотез (формула Байеса).

Если до опыта вероятности гипотез были Р(Н₁), Р(Н₂)…Р(Н_N), а в результате опыта произошло событие А, то условные вероятности гипотез находятся по формуле:

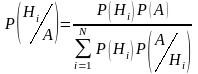
7. Повторение испытаний       Формула Бернулли 

где   - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

8. Общая теорема о повторении опытов

В отличие от частной теоремы она применяется когда вероятность появления каждого из событий не равны между собой

F(A₁)≠F(A₂) ≠F(A₃) ≠…

В этих случаях вероятности комбинаций приходится расписывать подробно. Так, вероятность появления одного любого из трех событий приходится вычислять по формуле:

При большом количестве n событий число комбинаций и, следовательно, число слагаемых существенно возрастает.

Для упрощения вычислений возможно применение производящей функции:

,

где p_i=F(A_i) – вероятность появления i-го события

q_i=1-F(A_i) – вероятность отсутствия i-го события

П - символ произведения

Для n=3 производящая функция равняется

При увеличении n количество сомножителей увеличивается. Результатом вычисления произведения является многочлен вида

j = a₀Z⁰+ a₁Z+ a₂Z²+ a₃Z³+ … + a_nZⁿ

где а₀, а₁, … а_n – коэффициенты при Z, представляющие числа из комбинаций q_i и p_i.

Каждый коэффициент численно равен вероятности появления такого количества событий, число которого равняется показателю степени Z. Так при отсутствии любого события показатель степени равняется 0, а вероятность равняется

При одновременном появлении всех n событий показатель степени равняется n, а вероятность равняется

Вероятность появления одного любого события из А₁, А₂, …, А_n будет равняться , а вероятность появления одновременно двух событий будет равняться F_n²=a₂ и т.д.

Применение производящей функции позволяет формализовать вычисление вероятностей появления событий и избежать применения более громоздкого математического аппарата теорем умножения и сложения

9.  Локальная теорема Лапласа. Если вероятность   появления события   в каждом испытании постоянна и отлична от нуля и единицы, то вероятность   того, что событие   появится в   испытаниях ровно   раз, приближенно равна (тем точнее, чем больше  ) значению функции

при

Имеются таблицы, в которых помещены значения функции

соответствующие положительным значениям аргумента  . Для отрицательных значений аргумента пользуются теми же таблицами, так как функция   четна, т. е.  .

Итак, вероятность того, что событие   появится в   независимых испытаниях ровно   раз, приближенно равна

где

10. Предельная интегральная теорема Муавра-Лапласа.

В условиях предыдущей теоремы вероятность того, что событие А в серии из n испытаний наступит не менее k₁ раз и не более k₂ раз:

- функция Лапласа

Следствие:

11. Закон распределения дискретной случайной величины

Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.

Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения).

Рассмотрим случайную величину X, которая принимает значения x1, x2, x3 ... xn с некоторой вероятностью pi, где i = 1.. n. Сумма вероятностей pi равна 1.

Таблица соответствия значений случайной величины и их вероятностей вида

x1	x2	x3	...	xn	...
p1	p2	p3		pn

12. Поток событий — последовательность событий, которые наступают в случайные моменты времени.

Поток событий называется стационарным, если вероятность попадания n событий на интервале времени (t,t+   ) зависит от   и не зависит от t. Это означает, что интенсивность потока событий не зависит от времени. Такие потоки событий часто встречаются на практике, об их стационарности строго можно говорить только на ограниченном интервале времени. Распространение этого участка до бесконечности - удобный прием.

Поток событий называется потоком без последействия, если для любых двух непересекающихся промежутков времени число событий попадающих в один из них не зависит от того, сколько событий попало в другой. Это означает, что события, образующие поток появляются независимо друг от друга, т.е. поток есть марковский процесс.

Поток событий называется ординарным, если вероятность осуществления на бесконечно малом отрезке времени t двух и более событий  (i=2,3,... пренебрежимо малы по сравнению с вероятностью   одного события

Поток событий называется простейшим, если он стационарен, однороден и не имеет последействия. Для такого потока вероятность появления на интервале   m событий определяется формулой Пуассона     -средняя интенсивность потока.

Для простейшего потока интервал t между соседними событиями имеет показательное распределение:  . Если рассматривать бесконечно малый временной интервал, то с учетом ординарности пуассоновского потока Поток событий называется рекуррентным или потоком "Пальма", если он стационарен, ординарен, а интервалы времени между событиями представляют собой независимые случайные величины с одинаковым произвольным распределением.

13. Математическое ожидание (МО)

М(х), МО(х), mx, m

Основные свойства МО:

1. М(х) СВ Х Þ Хmin£М(х)£Хmax

2. М(С)=С МО постоянной величины есть величина постоянная

3. М(Х±У)=М(Х) ±М(У)

4. М(Х×У)=М(х) ×М(у) Þ М(Сх)=СМ(х) – МО произведения двух независимых СВ

5. М(аХ+вУ)=аМ(Х)+вМ(У)

6. М(Х-m)=0 – МО СВ Х от её МО.

МО основных СВ

Дискретные Случайные Величины

1. Биноминальные СВ МО(Х)=np

2. Пуассоновские СВ МО(Х)=l

3. Бернуллиевы СВ МО(Х)=р

4. Равномерно распред. СВ

Непрерывные Случайные Величины

1. Равномерно распределенная СВ

2. Нормально распределенная СВ MO(X)=m

3. Экспоненциально распределенная СВ

14. Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

где:

 — значение моды

 — нижняя граница модального интервала

 — величина интервала

 — частота модального интервала

 — частота интервала, предшествующего модальному

 — частота интервала, следующего за модальным

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот   , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

Ме = (n(число признаков в совокупности) + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

где:

 — искомая медиана

 — нижняя граница интервала, который содержит медиану

 — величина интервала

 — сумма частот или число членов ряда

 - сумма накопленных частот интервалов, предшествующих медианному

 — частота медианного интервала

15. Начальные и центральные моменты

    Кроме характеристик положения — средних, типичных значений случайной величины, — употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяются так называемыемоменты.      Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т. д.). Cовершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.      Начальным моментом s-го порядка прерывной случайной величины Х

16.   Неравенство Чебышева.:

Для любой СВ с ограниченными первыми двумя моментами (есть МО и D) и для любого >0:

17. 

Требуется только знание дисперсии СВ при любом законе распределения.

18. Теорема Чебышева

При X₁, X₂, …, X_n – последовательность независимых СВ. Для любого >0 и n:

Из теоремы следует, что среднее арифметичес­кое случайных величин при возрастании их числа проявляет свойство устойчивости, т. е. стремится по вероятности к неслучайной величине, которой является среднее арифметическое математических ожиданий этих величин, т.е. вероятность отклонения по абсолютной величине среднего арифметического случайных величин от среднего арифметического их математических ожиданий меньше чем на e при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием.

19. Закон Больших Чисел устанавливает связь между абстрактными моделями теории вероятностей и основными ее понятиями и средними значениями, полученными при статистической обработке выборки ограниченного объема из генеральной совокупности. P, F(x), M(x), D(x)

ЗБЧ в форме Бернулли. m – число успехов в серии из n последовательных испытаний Бернулли. P – вероятность успеха в каждом отдельном испытании. >0:

ЗБЧ носит чисто качественный характер. В тех же условиях неравенство Чебышева позволяет получить количественную характеристику оценки вероятности.

Характеристическая функция fX (t) случайной величиныХ определяется как математическое ожидание величины eitX. Это определение для случайных величин, имеющих плотность вероятности pX (x), приводит к формуле .   Например, для случайной величины, имеющей нормальное распределение с параметрами а и s,Характеристическая функция равна

20. Как уже отмечалось, нормальные распределения в настоящее время часто используют в вероятностных моделях в различных прикладных областях. В чем причина такой широкой распространенности этого двухпараметрического семейства распределений? Она проясняется следующей теоремой.

Центральная предельная теорема (для разнораспределенных слагаемых). Пусть X₁, X₂,…, X_n,… - независимые случайные величины с математическими ожиданиями М(X₁), М(X₂),…, М(X_n), … и дисперсиями D(X₁), D(X₂),…, D(X_n), … соответственно. Пусть

Тогда при справедливости некоторых условий, обеспечивающих малость вклада любого из слагаемых в U_n,