2.4.4. Граничные условия

Уравнения Максвелла в дифференциальной форме (2.16), (2.17) справедливы для линейных сред, параметр ε которых либо не зависит от координат, либо является непрерывной функцией координат. На практике, часто рассматриваемая область состоит из двух (или более) разнородных сред. При анализе макроскопических свойств поля в этих случаях обычно приходится считать, что параметр ε на границе раздела сред меняется скачком. Операция дифференцирования в точках, принадлежащих границе раздела, незаконна, и уравнения Максвелла в дифференциальной форме в этих точках теряют смысл. Поэтому для изучения поведения векторов электромагнитного поля при переходе из одной среды в другую нужно исходить из уравнений Максвелла в интегральной форме, которые остаются справедливыми и в этих случаях. Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. Уравнения Максвелла не определяют электромагнитное поле полностью без задания граничных условий.

В задачах о неоднородных структурах без скачкообразного изменения граничным условием обычно является требование исчезновения поля в бесконечности и ограниченность поля внутри любой конечной области пространства. Требование отсутствия поля в бесконечности приводит к направляемым модам (типам волн), поле которых ограничено направляющей структурой (системой), при этом не теряется их мощность на излучение.

Наиболее общий тип граничных условий в световодных устройствах соответствует кусочно-однородному распределению ε. Представляют интерес граничные условия для переменных во времени полей. Искомые граничные условия получаются из уравнений Максвелла путем интегрирования их по объему, выбираемому на границе раздела сред. Стягивая объем в точку, в пределе получаем равенство тангенциальных составляющих электрического и магнитного полей на границе раздела сред:

Н_t1=H_t2, E_t1=E_t2 (2.49)

Физический смысл этих соотношений состоит в том, что тангенцианальные составляющие полей Н и Е непрерывны на границе раздела сред. Граничные условия совместно с условиями на бесконечности определяют конкретные решения уравнений Максвелла для конкретной задачи. При этом поля представляются в виде некоторых функций координат, частот и времени. В этом состоит волновой метод решения задач.

2 .4.5. Волновой анализ распространения мод

Проведем волновой анализ распространения мод на примере ОВ со ступенчатым ППП. Для этого рассмотрим ОВ без потерь двухслойной конструкции (рис. 2.19).

Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения.

В

Рис. 2.19. Конструкция ОВ

двухслойной структуры

олновое уравнение (2.40) в цилиндрической системе координат r, φ, z относительно компонентов электрического поля или магнитного поля Н_z изменяющихся во времени t и вдоль оси z волокна, в виде

(2.50)

переходит в уравнение Гельмгольца:

(2.51)

где (2.52)

χ - поперечное волновое число, или собственное значение; β— фазовая постоянная.

Для описания поведения электромагнитного поля в сердцевине (0<r<a) и в оболочке (а<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции сердцевины при r = 0 должны быть конечными, а в оболочке должны описывать спадающее поле. Используем цилиндрическую систему координат, ось которой совместима с осью цилиндра. Поверхностные составляющие напряженности электрического и магнитного полей могут быть выражены через продольные составляющие Е_z и Н_z. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с n₂ на рис. 2.19 простирается до бесконечности (d=∞). Такое упрощение модели является оправданным и приводит к адекватным характеристикам мод реального ступенчатого ОВ, имеющего защитное покрытие, обеспечивающее механическую защиту ОВ. В таком случае n в формуле (2.52) равно или n₁ в середине ОВ, или п₂ во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить

(2.53)

чтобы поле в радиальном направлении в среде п₂ убывало. Тогда решение уравнения (2.51) можно записать:

для сердцевины ОВ с показателем преломления n₁ в виде:

(2.54)

(2.55)

Зависимость всех полей от координат φ в виде cosnφ и sinnφ свидетельствует о том, что в волокнах круглого сечения моды на равных могут существовать в виде двух взаимно ортогональных поляризаций. Это значит, что моды в ступенчатом ОВ являются попарно вырожденными по поляризации, что особенно важно для передачи сигналов в одномодовом ОВ. Таким образом, решения (2.54) и (2.55) дают возможность изучить условия распространения волн в ступенчатом ОВ. В решениях (2.54) и (2.55) А_m, В_m, С_m и D_m — постоянные интегрирования; J_n, N_n — функции Бесселя первого и второго рода n-го порядка, соответственно; I_n и K_n –видоизмененные (модифицированные) функции Бесселя первого и второго рода п-го порядка, соответственно. Качественные характеристики функции в зависимости от собственных значений χ₁r и a₂r приведены на рис. 2.20.

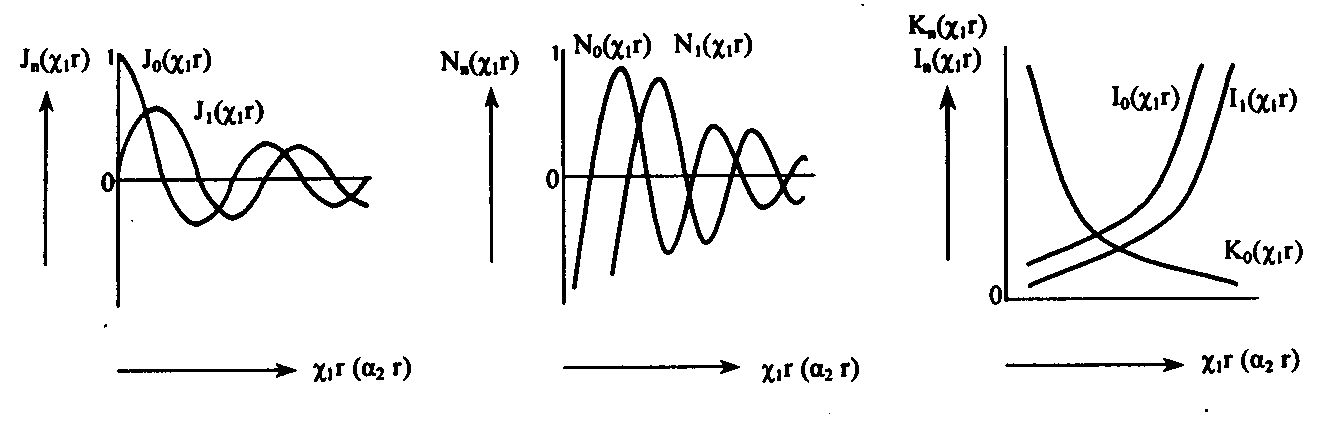
Рис. 2.20. Качественные зависимости функций J_n (χ₁r),

N_n(χ₁r), I_n(χ₁r) и K_n(χ₁r) от аргумента χ₁r(а₂r)

При r→0 значение N_n →-∞. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить В_m =0. Поле за пределами сердцевины должно убывать в радиальном направлении и при r→∞ должно стремиться к нулю. Однако I_n при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить C_m = 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция J_n(χ₁r) описывает распределение поля внутри сердцевины ОВ, а функция K_n(а₂r) описывает изменение поля за ее пределами (в среде с п₂) и ведет себя при больших значениях а₂r как exp( - а₂r). Тогда уравнения (2.54) и (2.55) перепишутся в виде:

(2.56)

(2.57)

Постоянные интегрирования А_т и D_т могут быть определены на основании граничных условий, как отмечалось ранее. Поперечные составляющие электрических (Е_r, Е_φ) и магнитных (Н_r, Н_φ)полей могут быть выражены с помощью известных соотношений между поперечными и продольными (Е_z, Н_z) составляющими. Тогда, используя условие равенства тангенцианальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина — оболочка (при r =a):

(2.58)

найдем постоянные интегрирования. Подставим их в уравнения типа (2.56) и (2.57), и после соответствующих преобразований получим следующее характеристическое уравнение:

(2.59)

Это уравнение позволяет определить структуру поля, параметры волн и характеристики ОВ. В общем случае оно имеет ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны, или модой. Обычно в ступенчатых ОВ, применяемых для линий передачи сигналов, n₁≈n₂. Тогда уравнение (2.59) можно переписать в виде:

(2.60)

В ступенчатом ОВ отсечка моды (критические условия) наступает при равенстве поперечного волнового числа в оболочке -α₂=0, это возможно при β=k₂. При этом условии из (2.60) следует, что

(2.61)

О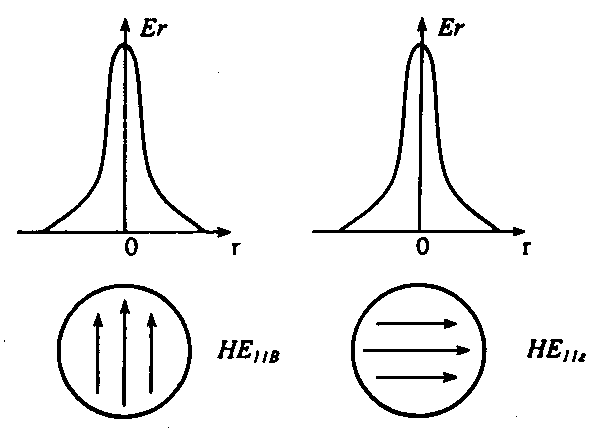 тсюда видно, что низшая (основная) мода (п=0) имеет отсечку, определяемую из уравнения:

П

Рис. 2.21. Пример двух взаимноортогональных поляризаций моды НЕ₁₁

ервый корень этого характеристического уравнения χ₁а= 0, и он соответствует моде НЕ₁₁. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ_11r и НЕ_11B соответствующих cosφ и sinφ (рис. 2.21). Распределение плотности поперечного поля в поперечном сечении сердцевины подчиняется закону J₀(χ₁r), приближающемуся к Гауссовому закону exp(–r²/ω₀²) распределения поля в лазерном световом пучке. Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J₁(χ₁r) второй раз становится равной нулю, т.е. когда χ₁а= 3,83 (рис. 2.22). Эта мода обозначается НЕ₁₂. Аналогично для n=0 следуют моды НЕ₁₃, НЕ₁₄…

В приведенных обозначениях мод первый индекс учитывает порядок функции, второй—номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя.

Следующая совокупность мод соответствует n=1 или характеристическому уравнению:

. (2.62)

Первым корнем этого уравнения является χ₁а=2,405. Ему соответствуют две волны Н₀₁ и E₀₁. Второму корню уравнения (2.62) соответствует следующая пара мод Н₀₂ и Е₀₂ и т.д.

В качестве примера значения части корней бесселевых функций P_пт = χ₁а в зависимости от порядка функций и корня бесселевой функции, приведены в табл. 2.3.

_{Таблица 2.3. Значения корней бесселевых функций Pпт}

Тип волны	Порядок функций, n	Pnm для номера корня функции, m
		1	2	3
Eom, Hom	0	2,405	5,520	8,654
HE11	1	0,000	3,832	7,016
EH1m	1	3,832	7,016	10,173
HE2m	2	3,05	5,538	8,665
EH2m	2	5,136	8,417	11,620

Таким образом, функции Бесселя первого рода п-гo порядка дают бесконечное число корней. Причем корни функции J₀(χ₁а) определяют структуру поля симметричных волн (E_om,H_om), а J_п(χ₁а) при п≠0 структуру несимметричных гибридных волн (EН_om,HЕ_om). В индексе моды п — число изменений поля по диаметру, а т — число изменений поля по периметру сердцевины ОВ.

Симметричные волны электрические E_om и магнитные H_om имеют круговую симметрию (n=0). Раздельное распространение по световоду несимметричных волн типа Е_пт и Н_пт невозмоно. В ОВ они существуют только совместно, т.е. имеются продольные составляющие Е и Н. Эти волны называются гибридными, дипольными и обозначаются через НЕ_пт, если поле в поперечном сечении напоминает поле Н, или E_пт, если поле в поперечном сечении ближе к волнам Е.