Подвійний векторний добуток
Означення 19. Подвійним векторним добутком векторів , , називається вектор |
Якщо
ввести позначення
,
то
.
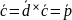Твердження
13.
Подвійний векторний добуток векторів
,
,
|
.
Доведення.
Введемо декартову систему спеціальним
чином. Вісь
спрямуємо вздовж вектора
,
а вісь
розмістимо в площині векторів
,
,
приведених до спільного початку. Тоді
матимемо наступні координати векторів:
,
,
.
Обчислимо
подвійний векторний добуток векторів
,
,
=
=
=
+
,
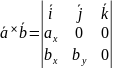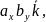
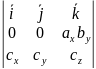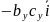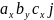але
,
+
,
=
+
,
=
+
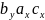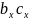Звідси
=-
+
,
тобто формула доведена.
Наведемо основні властивості подвійного векторного добутку:
Вектори ,
- компланарні.Подвійний векторний добуток не є переставним:
=-
При циклічній перестановці векторів матимемо формули:
;
;
.
Додавши ліві і праві частини останніх трьох співвідношень, одержимо тотожність Якобі:
-
=0
Приклад 6. Задано координати вершин трикутника А(-1,-2,4), В(-4,-2,0), С(3,-2,1). Визначити кут при вершині В і проекцію сторони АВ на сторону ВС.
Розв’язок.
Знайдемо координати векторів
,
що співпадають з відповідними сторонами
трикутника:
;
𝜑
між цими векторами визначаємо із
співвідношення:
=
.
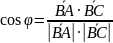П
роекцію сторони АВ на сторону ВС знайдемо як проекцію вектора
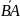на
напрямок вектора
:
=
=
.
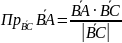П
риклад 7. Задано координати вершин піраміди: А(0,-1,2), В(2,1,1), С(-2,0,0), D(-1,1,0).
З найти: 1) Площу грані АВС.
2
) Об’єм піраміди.
Р
Рис. 3.1.18
озв’язок. Знайдемо координати векторів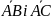
:
Далі обчислимо векторний добуток знайдених векторів:
=-3·
Як випливає з геометричного змісту, модуль цього векторного добутку дорівнює площі паралелограма, побудованого на векторах . Звідси площа грані АВС дорівнює:
=
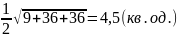
2)
Об’єм
піраміди
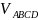знайдемо
як
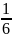об’єму
паралелепіпеда, побудованого на векторах
,
,
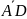тобто як
частину мішаного добутку цих векторів.
Маємо:
=0,5
(куб.од.)
Приклад
8.
Знайти координати вектора
в базисі
,
,
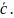
Розв’язок.
Враховуючи, що вектори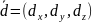
,
,
,
задані у декартовій системі координат
і вектор
є
лінійною комбінацією векторів
,
,
,
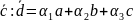обчислимо невідомі коефіцієнти
з наступних співвідношень:
+
+
⇨
(
)
(
)
(
)
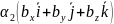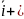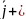Але ж два вектори рівні тоді, коли рівні їх координати:
+
+
=
+
+
=
+
+
=
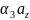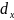
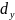
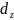
Маємо систему лінійних рівнянь відносно невідомих , що має єдиний розв’язок у випадку, коли її визначник не дорівнює нулю:
≠0
Якщо
вектори
,
,
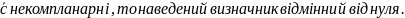
Розв’язуючи систему рівнянь відносно , одержимо за правилом Крамера координати вектора у базисі , , :
,
,
.
•
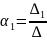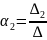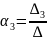Приклад
9.
Перевірити, чи утворюють вектори
;
,
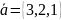базис? Якщо утворюють, то знайти координати
вектора
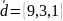в цьому базисі.
Розв’язок. Три вектори утворюють базис, якщо їх мішаний добуток не дорівнює нулю. Шляхом відповідного обчислення з’ясовуємо:
=
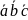=-23≠0.
Отже, вектори , , утворюють базис. Це означає, що всі інші вектори у тривимірному просторі можна виразити через цю трійку векторів.
Позначимо координати вектора в базисі , , через x, y і z.
Для знаходження координат вектора в новому базисі потрібно розв’язати систему рівнянь:
3x+y+2z=9
2x-2y+z=3
x-2y+3z=1
Розв’язуючи дану систему за допомогою формул Крамера, маємо:
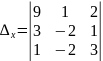=-46
=
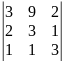=-23
=
=-23
=
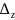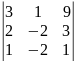-23⇨
,
,
=
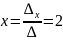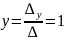1.
Отже,
.
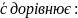
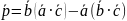