
- •§3.1. Вектори на площині і в просторі Означення і позначення векторів
- •Коленіарність і компланарність векторів
- •Лінійні операції над векторами
- •Проекція вектора на вісь
- •Властивості проекцій
- •Лінійна залежність векторів
- •Декартова (прямокутна) система координат
- •Скалярний добуток векторів
- •Властивості скалярного добутку
- •Скалярний добуток векторів, заданих у координатній формі
- •Векторний добуток
- •Властивості векторного добутку
- •Мішаний добуток векторів
- •Властивості мішаного добутку векторів
- •Подвійний векторний добуток
Декартова (прямокутна) система координат
З
твердження 2 випливає, що три не
компланарних вектора
 ,
,
 ,
,
 утворюють у просторі базис, тобто
будь-який інший вектор
може бути однозначно представлений
лінійною їх комбінацією:
утворюють у просторі базис, тобто
будь-який інший вектор
може бути однозначно представлений
лінійною їх комбінацією:
 +
+ +
+ .
При цьому встановлюється взаємооднозначна
відповідність між векторами простору
і трійками дійсних чисел (
.
При цьому встановлюється взаємооднозначна
відповідність між векторами простору
і трійками дійсних чисел ( ),
які називаються координатами вектора.
),
які називаються координатами вектора.
Трійка некомпланарних векторів , , зведена до спільного початку О утворює систему координат у просторі, яка називається афіною. |
На практиці найбільш уживаним є ортонормований базис, який складається з трьох взаємно перпендикулярних векторів одиничної довжини. При цьому розрізняють праві і ліві трійки векторів.
Означення 15. Трійка векторів називається правою (лівою), якщо з кінця вектора найкоротший поворот від вектора до вектора спостерігається проти (за) годинниковою стрілки (рис. 3.1.11, а). |
З
Рис. 3.1.12













Декартова (прямокутна) система координат у просторі (рис. 3.1.12) являє собою три взаємно перпендикулярні прямі Ох, Оy, Oz, які називаються координатними осями, з заданим на кожній з них додатнім напрямком, початком координат (точка перетину осей) і одиничним відрізком (масштабом). |
Вісь
 називається віссю абсцис, вісь
називається віссю абсцис, вісь
 – віссю ординат, а вісь
– віссю ординат, а вісь
 – віссю аплікат.
– віссю аплікат.
Одиничні
вектори координатних осей
 позначаються
відповідно:
,
(
позначаються
відповідно:
,
( ).
Оскільки вони є не компланарними, кожний
вектор простору може бути представлений
у вигляді:
).
Оскільки вони є не компланарними, кожний
вектор простору може бути представлений
у вигляді:
= |
, який називається розкладом вектора за координатними ортами.
З
рис. 3.1.12 видно, що якщо провести через
точку М площини, паралельні координатним
площинам
 ,
,
 ,
,
 ,
то одержимо
точки перетину з координатними осями
С, В, А, причому за правилом паралелепіпеда
матимемо:
,
то одержимо
точки перетину з координатними осями
С, В, А, причому за правилом паралелепіпеда
матимемо:
 .
.
Оскільки
розклад вектора за базисом
є однозначним, матимемо, що


Це означає, що координатами вектора у просторі є його проекції на координатні осі. |
З властивостей проекції вектора на вісь одержимо аналогічні властивості для векторів, заданих координатами:
Два вектори рівні тоді і тільки тоді, коли їх відповідні координати рівні:
 =
= ,
,
 .
.Координати вектора
 ,
який дорівнює сумі двох векторів
,
який дорівнює сумі двох векторів
 ,
і
,
і
 ,
дорівнюють сумі відповідних координат
цих векторів:
,
дорівнюють сумі відповідних координат
цих векторів:
 ,
,
 ,
, .
.
Координати вектора
 ,
який
дорівнює добутку вектора
,
який
дорівнює добутку вектора
 на
число λ,
дорівнюють координатам вектора
на
число λ,
дорівнюють координатам вектора
 помноженим
на це число:
помноженим
на це число:
 λ
λ λ
λ ,
,
 λ
λ ,
,
 λ
λ .
.
За означенням проекції вектора на вісь матимемо:

Косинуси кутів, які утворює вектор з осями координат, називаються напрямними косинусами вектора.
Вектор, проведений з початку координат О до точки простору М, називається радіус-вектором точки М.
Координатами
точки М називається упорядкована
трійка чисел (x,
y,
z),
які є координатами радіус-вектора
|
Вектор
(рис. 3.1.12) є діагоналлю прямокутного
паралелепіпеда, тому його довжина
дорівнює:
 .
(3.1.13)
.
(3.1.13)
Для напрямних косинусів вектора матимемо формули:
причому
|
Я
Рис. 3.1.13








кщо вектор має задані початкову А(
 )
і
кінцеву В(
)
і
кінцеву В( )
точки
у просторі (рис.3.1.13), то його координати
)
точки
у просторі (рис.3.1.13), то його координати
 визначаються з наступних міркувань.
Проведемо з початку координат О у точки
А і В радіус вектора
визначаються з наступних міркувань.
Проведемо з початку координат О у точки
А і В радіус вектора
 .
Тоді за правилом трикутника матимемо:
.
Тоді за правилом трикутника матимемо:
 .
Звідки
.
Звідки ,
або у координатній формі:
,
або у координатній формі:
|
Звідси
для довжини вектора

= |
(3.1.5)
Таким чином, кожній точці простору ставиться у відповідність трійка дійсних чисел, які є проекціями радіус-вектора точки на координатні осі. Справедливим є і обернене твердження: кожній трійці дійсних чисел (x, y, z) відповідає одна точка простору з такими координатами.
Прямокутна система координат на площині є частинним випадком тривимірної системи координат. Тому стисло наведемо основні положення і формули.
Твердження 7. Якщо будь-які два вектори на площині і неколінеарні, то вони утворюють базис на цій площині, і тоді будь-який вектор площини є лінійною комбінацією цих векторів:
|
Числа
 називаються координатами вектора
в базисі
,
,
що скорочено записується так:
називаються координатами вектора
в базисі
,
,
що скорочено записується так:
 .
.
На
практиці найбільш уживаним є ортонормований
базис, який складається з взаємно
перпендикулярних векторів одиничної
довжини, які мають позначення
Рис.
3.1.14
 ,
)
,
)
 ,
,
 .
Тоді на основі т
.
Тоді на основі т

 ,
де
,
де
 -
декартові (
-
декартові ( прямокутні)
координати вектора
(рис. 3
прямокутні)
координати вектора
(рис. 3
 проведеного
з
проведеного
з
З прямокутного трикутника ОМА визначаємо напрямні косинуси:
|
,
|
|
= |
І модуль вектора
(3.1.7)
Таким чином вектор у просторі можна задати:
Зображенням вектора в просторі як напрямного відрізка (рис. 3.1.15, в).
За допомогою координат:
 (рис. 3.1.15, б).
(рис. 3.1.15, б).За допомогою модуля і орта : .
За допомогою модулів і напрямних косинусів:
 (рис.
3.1.15, а).
(рис.
3.1.15, а).


z
z
z

y



y
y
х
х
х
Рис. 3.1.15

 +
+ +
+
 точки М.
точки М. ,
,
 ,
,
 ,
,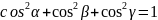 (3.1.4)
(3.1.4) .
.
 +
.
+
.

