5.2.2 Параметры замедляющих систем

Дисперсионные свойства замедляющих систем. Поскольку основное применение замедляющих систем связано с применением в электронных приборах СВЧ, в основе которых лежит принцип синхронизма электронов с полем бегущей электромагнитной волны, то одной из важных характеристик их является зависимость фазовой скорости от частоты или дисперсионная характеристика. Действительно, если фазовая скорость сильно изменяется с частотой, синхронизм для электронов, обладающих данной скоростью, возможен лишь в весьма узкой полосе частот, и такой прибор вряд ли будет обладать широкополосностью. Напротив, малая дисперсия является необходимым тре­бованием для осуществления взаимодействия в широкой полосе частот.

Хорошей в этом отношении является спираль с большим замедлением, дисперсия которой может сохраняться малой даже при значительном изменении частоты.

По виду зависимости замедляющие системы могут быть подразделены на системы с нормальной дисперсией и системы с аномальной дисперсией.

Признаком нормальной дисперсии является уменьшение фазовой скорости с повышением частоты. Такой дисперсией обладают, напри­мер, спираль, гребенка и диафрагмированный волновод. Аномальная дисперсия соответствует нарастанию фазовой скорости с повышением» частоты. К замедляющим системам с аномальной дисперсией относится, например, система со встречными гребенками, изображенная на рис. 6,б.

При изучении распространения волн в замедляющих системах основное внимание уделяется вопросу о фазовой скорости, так как именно она ответственна за синхронизм волн с электронами пучка. Однако, кроме фазовой скорости, волна может быть охарактеризована еще и групповой скоростью, которая определяет скорость переноса энергии волной. Групповая скорость

(7)

может быть легко найдена, если задана зависимость . Если же, как это чаще бывает, задается зависимость , групповая скорость может быть найдена путем несложного расчета:

где

Подставляя найденную производную в предыдущее выражение, получим формулу Рэллея

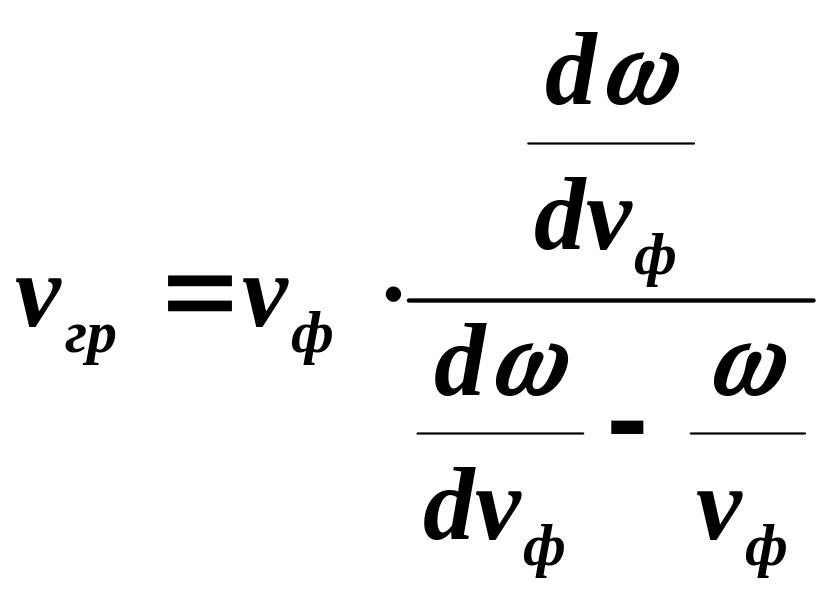(8)

Выражение (8) позволяет сделать важные заключения о соотношении групповой и фазовой скорости для различных видов дисперсии. Так, например, для системы, обладающей нормальной дисперсией, зави­симость всегда будет иметь вид спадающей кривой (рис.10,а).

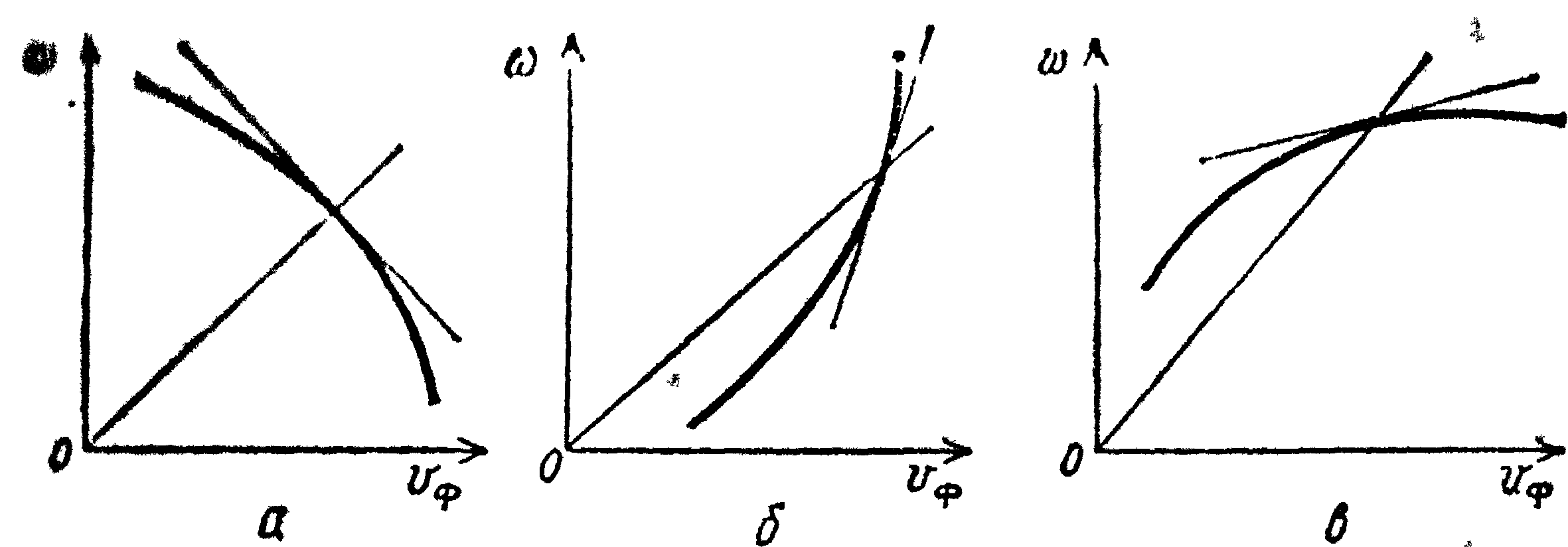
Рис.10

Положительному наклону секущей в этом случае будет соответ­ствовать отрицательный наклон касательной . Числитель и знаменатель (8) имеют один знак (в данном случае отрицательный), и знак групповой скорости соответствует знаку фазовой. Это указы­вает, что направление распространения энергии должно совпадать с направлением перемещения фазы. Но абсолютное значение числителя при этом получается меньше абсолютного значения знаменателя, так что в случае нормальной дисперсии величина групповой скорости всег­да меньше фазовой.

При аномальной дисперсии кривая является восходящей (рис. 10, б, в), так что секущая и касательная имеют наклон одного и того же знака. При этом встречаются два различных случая.

1. Наклон касательной больше наклона секущей (рис. 10, б), > . В этом случае числитель и знаменатель в выражении (8) получаются одинакового знака, но числитель оказывается больше знаменателя. Это значит, что направления фазовой и групповой ско­ростей совпадают, однако групповая скорость по величине превышает фазовую.

2. Наклон касательной меньше наклона секущей (рис. 10, в), < . Здесь знаки числителя и знаменателя различны. Это значит. что направление групповой скорости должно быть противополож­но направлению фазовой. Такая дисперсия носит название отрицатель­ной (в отличие от положительной дисперсии, где направления и совпадают). Абсолютное значение | | может быть как больше, так и меньше | |.

Таким образом отрицательная дисперсия может быть как положительной, так и отрицательной.

Сопротивление связи. Электронный пучок, взаимодействующий с полем замедляющей системы, находится на некотором расстоянии. Поэтому электрическое поле, действующее на электроны, отличается от поля вблизи замедляющей системы. Для количественной характеристики степени связи поля спирали с электронным пучком вводится специальная величина, носящая название сопротивление связи :

,

- амплитуда продольной компоненты напряженности поля в области пространства, где проходит пучок; мощность, переносимая вдоль оси спирали. /

Для эффективного взаимодействия пучка с полем замедленной волны всегда желательно, чтобы сопротивление связи было возможно большим. Однако добиться этого обычно трудно, так как электрическое поле и достигает наибольшей напряженности у самой поверхности замедляющей системы. Чтобы не допустить попадания электронов пучка на замедляющую систему, пучок приходится пропускать на достаточно большом расстоянии от ее поверхности.

Точное выражение для сопротивления связи на оси спирали имеет довольно сложный вид. Однако в случае использования в качестве замедляющей системы спирали, у которой достаточно велико, оно может быть приведено к сравнительно простому виду: