Глава 6 Приборы с длительным взаимодействием электронов и свч-поля типа м.

Особое место в электронике СВЧ занимает класс приборов, в которых электрическое поле (его постоянная и высокочастотная сопоставляющие) направлено перпендикулярно к постоянному магнитному полю. По названию первого из приборов подобного рода — магнетрона — весь этот класс носит название приборов магнетронного типа, или приборов типа М. В отличие от рассмотренных выше приборов типа О, в которых постоянное магнитное поле направлено параллельно основной компоненте высокочастотного электрического поля и магнитное поле играет лишь вспомогательную роль для удержания электронных пучков от разбухания и в принципе может отсутствовать вообще, в приборах типа М магнитное поле определяет характер движения электронов в высокочастотном поле и является необходимым элементом для их функционирования.

Отличительной особенностью приборов магнетронного типа, выделяющей их изо всех остальных приборов СВЧ, является их весьма высокий электронный к. п. д., достигающий в отдельных случаях 70— 90 %. Это предопределяет применение приборов типа М в тех случаях, когда главным требованием оказываются высокая мощность и эффективность.

Приборы типа М были первыми приборами диапазона СВЧ, с помощью которых были получены колебания большой мощности. Еще в 1924—1927 гг. А.А. Слуцкиным и Д. С. Штейнбергом были созданы образцы магнетронов, работающих в дециметровом и сантиметровом диапазонах длин волн. Дальнейшее развитие этих исследований привело в 1936—1939 гг. к созданию Н. Ф. Алексеевым, Д. Е. Маляровым и В. П. Ильясовым первых многорезонаторных магнетронов диапазона СВЧ. Эти конструкции стали прототипом всех современных приборов типа М.

6.1 Физические основы приборов типа м

6.1.1 Движение электрона в скрещенных электрическом и магнитном полях в статическом режиме

Рассмотрим движение электрона, двигающегося со скоростью (см. рис.6.1), расположенной в плоскости x-y. На электрон действуют постоянное электрическое поле с напряженностью , расположенной в плоскости x-y и магнитное поле с индукцией , направленной перпендикулярно плоскости x-y.

Рис.6.1

Рассмотрим вначале движение электрона при отсутствии электрического поля. Будем рассматривать нерелятивистское движение электрона, т.е. , где с - скорость света. Поскольку сила Лоренца перпендикулярна скорости движения , то ее работа равна нулю и следовательно абсолютное значение и кинетическая энергия остаются постоянными . Поэтому является центростремительной силой и равна по модулю . Центробежная сила , где - угловая скорость движения по окружности радиуса (см. рис.6.2). Из равенства получаем , .

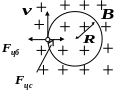
Рис.6.2

Для определения движения при наличии электрического поля воспользуемся уравнением Лоренца:

Одно из решений этого уравнения является движение с постоянной скоростью .

В этом случае уравнение Лоренца превращается в равенство . Откуда

. Поскольку любую скорость можно представить в виде , то уравнение Лоренца превращается в уравнение :

(6.1)

Это уравнение описывает движение электрона со скоростью в постоянном магнитном поле с магнитной индукцией , т.е. движение по окружности. Таким образом движение электрона можно представить в виде движения по окружности со скоростью . Причем центр окружности ( будем называть ведущий центр) смещается с постоянной скоростью , которую часто называют переносной скоростью (см. рис.6.3).

Рис.6.3

В координатной форме движение центра описывается следующими уравнениями:

, (6.2)

где , - координаты начальной точки движения, - радиус окружности, - угол между осью и направлением скорости в начальной точке движения, и проекции переносной скорости на ось x и ось y, соответственно.

Движение электрона по окружности в координатной форме можно представить в виде следующих уравнений:

. (6.3)

Рассмотрим несколько частных случаев движения:

1. Электрическое поле направлено по оси , . Индукция магнитного поля направлена по оси , .Электрон в начальный момент времени имеет координаты , а начальная скорость . В этом случае . А движение электрона представляет движение точки, находящейся на ободе колеса радиусом , где , , , как изображено на рис. 6.4. Кривая носит название циклоида.

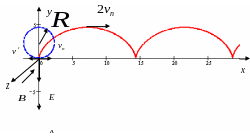
Рис. 6.4

2. Электрическое поле направлено по оси , . Индукция магнитного поля направлена по оси , . Электрон в начальный момент времени имеет координаты , а начальная скорость , . В этом случае . А движение электрона представляет движение точки, находящейся на ободе внутреннего колеса радиусом , соединенного с внешним колесом радиуса , как изображено на рис.6.5. В этом случае , , . Кривая движения носит название укороченная циклоида.

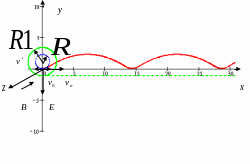
Рис. 6.5

При циклоида вырождается в прямую линию.

3. Электрическое поле направлено по оси , . Индукция магнитного поля направлена по оси , . Электрон в начальный момент времени имеет координаты , а начальная скорость . В этом случае . А движение электрона представляет движение точки, находящейся на ободе внешнего колеса радиусом , соединенного с внутренним колесом радиуса , как изображено на рис.6. 6. В этом случае , , . Кривая движения носит название удлиненная циклоида.

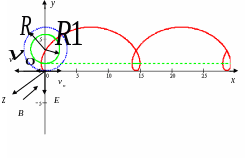
Рис. 6.6

4. Электрическое поле лежит в плоскости , . Индукция магнитного поля направлена по оси , . Для решения задач этого класса достаточно перейти к новой системе координат, в которой электрическое поле будет направлено по оси . В этой новой системе координат движение будет осуществляться по циклоидам, как в примерах 1-3. На рис.6.7 приведен пример такого движения.

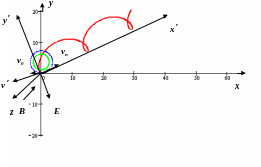
Рис. 6.7

6.1.2 Движение электрона в скрещенных электрическом и магнитном полях в статическом режиме при наличии СВЧ поля.

Предположим, что в пространстве между двумя электродами кроме скрещенных статических полей имеется еще СВЧ поле. Для создания этого поля используется замедляющая система, как изображено на рис.6. 8.

Рис.6.8

В общем случае СВЧ поле можно представить суммой пространственных гармоник, имеющих различные фазовые скорости. Обычно в приборах типа М используют нулевую пространственную гармонику, имеющей фазовую скорость равную фазовой скорости основной волны. Фазовая скорость волны, изображенной на рис.6. 8, равна ( здесь - фазовый набег на пространственный период равен , , - временной период волны). Переменные поля на рис.6. 8 изображены значком ’ ~’.

Для исключения зависимости электрических полей от времени перейдем к подвижной ( штрихованной) системе координат:

, , . (6.4)

Переход к штрихованной системе координат приводит к появлению некоторого дополнительного постоянного электрического поля . Появление этого поля связано с движением электрона в магнитном поле. Рассмотрим механизм появления этого поля более подробно.

Пусть есть неподвижная система координат, в которой электрон обладает некоторой скоростью и на него воздействует магнитное поле с индукцией . Электрон в этом случае будет двигаться по окружности радиуса с угловой скоростью , как изображено на рис. 6.2. Переход в двигающуюся систему координат (6.4) означает, что электрон двигается по окружности, центр которой двигается с переносной скоростью . То есть движение осуществляется по циклоиде. Например, как изображено на рис. 6.9 для начальных условий , , .

Рис. 6.9.

В соответствии с (6.2) и (6.3) для обеспечения такого движения необходимо электрическое поле , которое определяет переносную скорость . Для получаем .

Таким образом в двигающейся системе координат на электрон будет воздействовать магнитное поле с индукцией В и постоянное электрическое поле с напряженностью:

, (6.5)

г де , как изображено на рис. 6.10.

Рис. 6.10.

Электрон под воздействием этих полей будет двигаться по “квазициклоидным “ траекториям. Переносная скорость ведущего центра определяется по формуле:

, (6.6)

а радиус движения по формуле:

, (6.7)

где - угловая скорость вращения, , - начальная скорость электрона в штрихованной системе координат. Поскольку напряженность поля зависит от координаты электрона , то переносная скорость электрона и радиус движения

также будут зависеть от координаты . В частном случае, когда ( ) переносная скорость будет перпендикулярна . То есть ведущий центр двигается по эквипотенциальным линиям электрического поля , как изображено на рис. 6.11.

а)

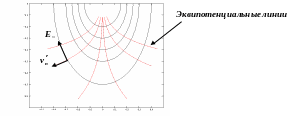
б)

Рис.6.11.

Как видно из рис. 6.11 в зависимости от направления поля электрон может двигаться от катода к аноду, приближаясь к осевой линии симметрии эквипотенциальных линий

( , рис. 6.11, а), так и от анода к катоду ( , рис. 6.11, б). Обычно первый случай движения принято называть движением электрона в благоприятной фазе. Второй случай движения - движением электрона в неблагоприятной фазе. Если , то электроны двигаясь от катода к аноду будут сближаться, но центр «сгустка» будет смещен относительно осевой линии симметрии эквипотенциальных линий, как изображено на рис. 6.12 для благоприятной фазы движения.

а)

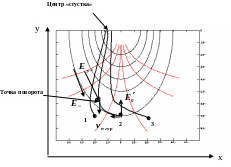
б)

Рис. 6.12

Такое смещение объясняется тем, что электрическое поле создает переносную скорость , направленную вдоль оси x. Поэтому электроны («1», «2», «3» на рис. 6.12) смещаются вдоль оси x, попадая в область, где есть горизонтальная составляющая электрического поля и вертикальная составляющая электрического поля . За счет электроны поднимаются вверх к аноду. За счет электроны двигаются в горизонтальном направлении. Вертикальная составляющая электрического поля растет при приближении к аноду. В некоторой точке «поворота» становиться равной и электрон прекращает горизонтальное движение. Вертикальное движение при этом остается. Поэтому выше точки поворота становиться больше и появляется горизонтальное движение в обратном направлении. Однако, если максимальное значение вертикальной составляющей электрического поля будет меньше , то «поворота» электрона не будет, и электрон будет двигаться вдоль оси x в одном направлении, как изображено на рис. 6.13.

Рис. 6.13.

В результате такого движения электрон перемещается из благоприятной фазы в неблагоприятную фазу и начинает двигаться от анода к катоду.