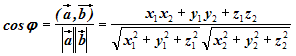- •1.Определите 2-го порядка. Их св-ва. Правила вычисления.
- •2.Определители 3-го порядка. Методы вычисления.
- •3.Системы м линейных n неизвестных. Основные понятия и решения.
- •4.Определение матрицы. Классификация матриц. Действия над ними.
- •5.Определение обратной матрицы, ее св-ва. Вычисление обратной матрицы.
- •6.Ранг матрицы
- •8.Понятие о линейной зависимости и независимости (векторов).
- •9.Теорема о ранге матрицы, ее следствие.
- •10.Вычисление обратной матрицы с помощью элементарных преобразований.
- •11.Теорема Кронекера Капелли. (о совместности решения сист.)
- •12.Однородные сист. Линейных ур-й. Их св-ва.
- •13.Метод Гаусса. Решение сист. Линейных алгебраических ур-й этим методом.
- •14.Векторы. Основные определения.
- •15.Линейные операции над векторами.
- •16.Определение проекция вектора.
- •17.Теоремы о проекциях векторов.
- •18.Скалярное произведение векторов. Его св-ва.
- •19.Длина вектора, расстояние между точками.
- •20.Угол между двумя векторами. Направление косинуса (cos) вектора.
- •21.Условие параллельности и перпендикулярности векторов.
- •22.Деление отрезка в данном отношении.
- •23.Векторное произведение векторов. Его св-ва.
- •24.Выражение векторного произведения через проекции векторов.
- •25.Смешанное произведение векторов и его св-ва.
- •26.Объем параллелепипеда и пирамиды с помощью смешанного произведения векторов.
- •27.Прямая линия на плоскости.
- •28.Исследование общего ур-я прямой.
- •30.Угол между двумя прямыми.
- •32.Расстояние от точки до прямой.
- •34.Исследование общего ур-я плоскости.
- •36.Условие параллельности и перпендикулярности плоскостей.
- •37.Расстояние от точки до плоскости
- •38.Прямая в пространстве
- •39.Угол между двумя прямыми в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
- •40.Угол между прямой и плоскостью
- •41.Условие перпендикулярности и параллельности прямой и плоскости.
- •42.Вывод ур-й кривых 2-го порядка. (окружность, эллипс, гипербола, парабола)
- •42.Поверхности 2-го порядка
- •45.Модуль действительного числа. Его св-ва.
- •46. Числовая последовательность. Предел числовой последовательности.
- •48.Бесконечно малые и бесконечно большие ф-и и их св-ва.
- •49.Основные теоремы о пределах: предел суммы, разности, произведения, частного
- •50.Замечательные пределы
- •51.Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых(табл.).
- •52. Определение непрерывности ф-и в точке. Классификация точек разрыва.
- •55.Понятие производной. Геометрический и физический смысл производной.
- •Геометрический смысл производной.
- •3. Физический смысл производной.
- •56.Необходимые условия существования производной.
- •57.Вывод формулы производной от элементарных ф-й.(в тетради)
- •58.Дифференцирование ф-й заданных неявно и параметрически.
- •21.2. Функция, заданная параметрически
- •59.Дифференциал ф-и. Ее геометрический смысл. Св-ва. Таблица дифференциалов.
- •Свойства дифференциала аналогичны свойствам производной.
- •60.Производная и дифференциал высших порядков.
- •61.Формула приближенного вычисления ф-и.
- •62.Теоремы о среднем: Ферма, Ролля, Лагранжа, Каши.
- •3. Теорема Коши
- •64.Выпуклость, вогнутость, точки перегиба графика.
- •65.Асимптоты графика ф-и.
- •66.Общая схема исследования ф-и и построение графика.
16.Определение проекция вектора.
Проекцией
вектора
![]() на
ось
на
ось
![]() называется
длина отрезка A'B',
заключенного между проекциями конца и
начала вектора на эту ось. Этой длине
приписывается знак плюс, если направление
отрезка A'B'
совпадает с направлением оси, и знак
минус, если его направление противоположно
направлению оси.
называется
длина отрезка A'B',
заключенного между проекциями конца и
начала вектора на эту ось. Этой длине
приписывается знак плюс, если направление
отрезка A'B'
совпадает с направлением оси, и знак
минус, если его направление противоположно
направлению оси.
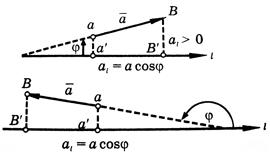
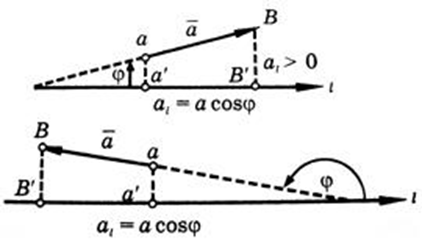
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).
Проекция
вектора
![]() на
ось
на
ось
![]() обозначается
через al
или
обозначается
через al
или
![]() ,
а угол между осью
и
вектором
будем
обозначать так:
,
а угол между осью
и
вектором
будем
обозначать так:
![]()
![]() .
Таким образом,
.
Таким образом,
![]()
![]()
![]() (2)
(2)
Если
![]()
![]() -
углы, образованные вектором
с
координатными осями Ox,
Oy
и Oz
прямоугольной системы координат, то
проекции вектора
на
координатные оси будут равны
-
углы, образованные вектором
с
координатными осями Ox,
Oy
и Oz
прямоугольной системы координат, то
проекции вектора
на
координатные оси будут равны
![]()
![]()
![]() (3)
(3)
В дальнейшем предполагается, что система координат - прямоугольная.
Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле
![]()
![]() (4)
(4)
т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.
Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).
Если
векторы
![]() и
и
![]() равны,
то равны и их проекции:
равны,
то равны и их проекции:
a1x = a2x; a1y = a2y; a1z = a2z. (5)
Если
для вектора
![]() известны
координаты его начала A(x1,
y1,
z1)
и координаты его конца B(x2,
y2,
z2),
то проекции вектора
на
координатные оси определяются по
формулам
известны
координаты его начала A(x1,
y1,
z1)
и координаты его конца B(x2,
y2,
z2),
то проекции вектора
на
координатные оси определяются по
формулам
ax = x2 - x1; ay = y2 - y1; az = z2 - z1, (6)
а модуль вектора в этом случае определится по формуле
![]()
![]() (7)
(7)
Очевидно, что по формуле (7) следует вычислять и расстояние между точками A(x1, y1, z1) и B(x2, y2, z2).
13. Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось.
Из векторного равенства
![]()
![]()
![]() (8)
(8)
следуют такие три скалярные равенства:
ax = a1x + a2x + a3x + ... + anx; ay = a1y + a2y + a3y + ... + any; (9) az = a1z + a2z + a3z + ... + anz.
17.Теоремы о проекциях векторов.
Т1. Проекция суммы векторов на некоторую числовую ось = сумме их проекций на ту же самую числовую ось.
18.Скалярное произведение векторов. Его св-ва.
Определение.
Под скалярным произведением двух векторов и понимается число, равное произведению длин этих векторов на косинус угла между ними:
.![]()
Праb=|b|×COS<α
Свойства скалярного произведения :
1. Переместительное свойство (комутативность):
![]()
2. Распределительное свойство(дистрибутивность):
![]()
3. Скалярный квадрат вектора равен квадрату модуля этого вектора:
![]()
4. Скалярный множитель можно выносить за знак скалярного произведения (ассоциативность):
![]()
5. Скалярное произведение линейной комбинации векторов на произвольный вектор равно скалярному произведению такой же линейной комбинации данных векторов на этот вектор:
![]() где
λ
и μ
- числа.
где
λ
и μ
- числа.
Геометрические св-ва:
6.![]() ;
;
![]() =±|
=±|![]() |
|
7.![]() =
|a|2
=
|a|2
6)
![]()
Скалярное произведение векторов в координатной форме.
Пусть
![]() .
Так
как
.
Так
как
![]() ,
то перемножая эти векторы и учитывая
соотношения:
,
то перемножая эти векторы и учитывая
соотношения:
![]() и
и
![]() ,
получаем
,
получаем
![]()
Отсюда, обозначая через φ угол между векторами и , будем иметь :