5.Определение обратной матрицы, ее св-ва. Вычисление обратной матрицы.

Если существует матрица Х такая, что АХ = ХА = Е, где Е – единичная матрица, то матрица Х называется обратной по отношению к матрице А, а сама матрица А – обратимой. Обратная матрица для А обозначается А^-1.

Св-ва обратной матрицы:

• Обратная матрица является обратимой

• Обратима только квадратная матрица

• Обратимость означает нахождение обратной матрицы

• Не всякая А-квадратная матрица будет обратимой, а именно А будет обратимо если:

1. АА^-1= А^-1А=Е

2. |А|≠0

3. А^-1≠0; |A||А^-1 |=1

Матрица называется особенной, если определитель равен нулю. (и наоборот)

Теорема

Для обратимости матрицы А (нахождения А^-1 )необходимо и достаточно что бы А была неособенной (|A|≠0).

1. Необходимость вытекает из св-ва обратной матрицы А^-1А=Е

Пусть |A|≠0; обозначим элемент а_ij – элемент матрицы А, покажем что А^-1 будет являться эл. Следующего вида а_ij^-1= А_ij/∆

Формула нахождения обратной матрицы

А^-1=1/ |A|А* А*=

Это матрица, состоящая из алгебраических дополнений транспонированной матрицы.

• Найти определитель матрицы |А|≠0;

• Найти алгебраически дополнения и транспонировать, то есть найти А*.

• Проверить АА^-1= А^-1А=Е.

6.Ранг матрицы

Рангом матрицы наз-ся наивысший порядок ее миноров отличных от 0. Если r – ранг матрицы, то найдется хотя бы один минор r порядка отличный от 0. Все миноры r+1 порядка будут = 0. Если ранг матрицы = r, то в этой матрице можно найти r линейно независимых между собой строк, через которые линейно выражаются все остальные ее строки.

7.Элементарные преобразования матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

Рассмотрим прямоугольную матрицу mхn. Выделим в этой матрице какие-нибудь k строк и k столбцов, 1  k  min (m, n). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами матрицы. Например, для матрицы можно составить миноры второго порядка и миноры первого порядка 1, 0, -1, 2, 4, 3.

Определение. Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы. Обозначают ранг матрицы r (A).

В приведенном примере ранг матрицы равен двум, так как, например, минор

Ранг матрицы удобно вычислять методом элементарных преобразований. К элементарным преобразованиям относят следующие:

1)     перестановки строк (столбцов);

2)     умножение строки (столбца) на число, отличное от нуля;

3)     прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Эти преобразования не меняют ранга матрицы, так как известно, что 1) при перестановке строк определитель меняет знак и, если он не был равен нулю, то уже и не станет; 2) при умножении строки определителя на число, не равное нулю, определитель умножается на это число; 3) третье элементарное преобразование вообще не изменяет определитель. Таким образом, производя над матрицей элементарные преобразования, можно получить матрицу, для которой легко вычислить ранг ее и, следовательно, исходной матрицы.

Пример 14. Найти ранг матрицы

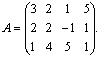
Решение. Поменяем местами строки матрицы, поставив последнюю строку на место первой:

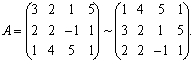
Умножим первую строку на –3 и прибавим ко второй. При этом на месте элемента 3 получим 0. Затем умножим первую строку на –2 и прибавим к третьей:

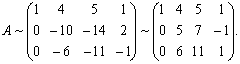
Умножим вторую строку получившейся матрицы на –1 и прибавим к последней, тогда

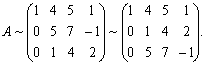
Умножим теперь вторую строку на –5 и прибавим к последней:

Преобразования матрицы можно прекратить, так как, очевидно, минор 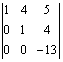, являющийся определителем треугольного вида, равен произведению элементов главной диагонали, то есть отличен от нуля. Следовательно, r (A)=3.