49.Основные теоремы о пределах: предел суммы, разности, произведения, частного

Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных:

.

 Доказательство.

 Проведем доказательство для двух слагае­мых, так как для любого числа слагаемых оно проводится так же. Пусть , . Тогда на основании теоремы можем написать:

,  ,где  и —бесконечно малые. Следовательно,

.

 Так как  есть постоянная величина, а - величина бесконечно малая, то снова по теореме заключаем, что

.

  Теорема  2. 

 Предел произведения двух, трех и вообще определенного числа переменных равен произведению пределов этих переменных

 

.

 Доказательство.  Для сокращения записи приведем доказательство для двух множителей. Пусть , . Следовательно,

, ,

.

Произведение , есть величина постоянная. Величина  на основании теорем есть величина бесконечно малая. Следовательно, .

 Следствие. Постоянный множитель можно выносить за знак предела.

 Действительно, если , с—постоянная и, следовательно,  , то ,  ч. т. д.

 Теорема 3.

 Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля:

, если .

 Доказательство. 

 Пусть , . Следова­тельно, , где  и  - бесконечно малые.

 Напишем тождества 

,

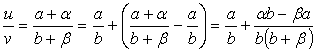
и ли Дробь  есть постоянное число, а дробь  по теоремам есть бесконечно малая переменная величина, так как  есть бесконечно малая, а знаменатель  имеет пределом .

Следовательно, .

50.Замечательные пределы

первым замечательным пределом называется предел        

Непосредственное вычисление предела

приводит к неопределённости вида .    Из геометрических соображений имеем S_DOAС< S_OAC < S_DOBC. Используя формулы площадей рассматриваемых фигур, получим

или

sin x < x < tg x

Разделив все части неравенства на sin x > 0, получим при условии х > 0

,

или

.

Так как функция у = cos x непрерывна, то

.

Пользуясь теоремой о пределе промежуточной функции, получим окончательно

.

  Замечание. Если х < 0, то знаки неравенств изменяются на противоположные, выводы же остаются прежними. 

Второй замечательный предел

  Ранее для натурального n было доказано

.

  Докажем, что для любого действительного x имеет место так же равенство

.

  Доказательство. Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем

.

Прибавим ко всем частям неравенств единицу

.

По свойству степеней имеем

Так как

и

,

то по теореме о пределе промежуточной функции имеем также и

,

что и требовалось доказать. Для отрицательного х доказательство аналогично. 

51.Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых(табл.).

таблица эквивалентных бесконечно малых при

Как показывает приведённый выше пример 2.36, пределы отношения бесконечно малых можно упрощать, откидывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные бесконечно малые. Для того, чтобы этот способ вычисления пределов (точнее, раскрытия неопределённостей вида ) можно было применять к возможно большему числу примеров, мы должны иметь достаточно большой запас известных пар эквивалентных бесконечно малых величин. Для наиболее употребительной базы создадим такой запас в виде таблицы "стандартных" эквивалентных бесконечно малых.

Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи обозначение этой базы будем пропускать и писать знак вместо .

1) . Эту формулу мы уже доказали и использовали в примерах. Эквивалентность и при означает в точности, что первый замечательный предел равен 1.

2) . Эта эквивалентность тоже была доказана выше в одном из примеров.

3) . Докажем эту эквивалентность:

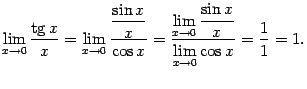
4) . Докажите это в качестве упражнения, сделав замену и применив предыдущую табличную формулу.

5) . Для доказательства воспользуемся формулой . Далее, имеем:

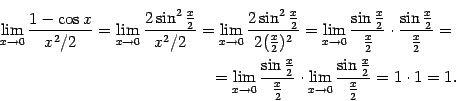
Это означает, что доказываемая эквивалентность имеет место.

6) ( ). Для доказательства этой эквивалентности сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

и мы доказали формулу 6.

В частном случае, при , получаем эквивалентность

) .

7) ( ). Для доказательства сделаем замену и выразим через : . Согласно формуле 6, при , откуда . Из непрерывности логарифма следует, что и, значит, при . В этой формуле осталось лишь сменить обозначение переменного на , чтобы получить формулу 7.

В частном случае, при , получаем эквивалентность

) .

Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней .

1)	.
2)	.
3)	.
4)	.
5)	.
6)	( ).
)	.
7)	( ).
)	.

    Сравнение бесконечно малых

Пусть и — бесконечно малые при . 1. Если , то говорят, что является бесконечно малой высшего порядка по сравнению с . В этом случае пишут . 2. Если , где —число, отличное от нуля, то говорят, что и — бесконечно малые одного и того же порядка. В часности, если , то бесконечно малые и называются эквивалентными. Запись ~ означает, что и —эквивалентные бесконечно малые.          Если , то это означает, что . Таким образом, является бесконечно малой высшего порядка по сравнению с , т. е. 3. Если и —бесконечно малые одного и того же порядка, причем , то говорят, что бесконечно малая имеет порядок по сравнению с . Отметим некоторые свойства бесконечно малых величин: 1o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если , то и . 2o. Бесконечно малые и эквивалентны тогда и только тогда, когда их разность является бесконечно малой высшего порядка по сравнению с и , т. е. если , . 3o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если , ~ , ~ , то .         Полезно иметь в виду эквивалентность следующих бесконечно малых величин: если , то ~          ~          ~          ~ ~          ~          ~