
- •1.Определите 2-го порядка. Их св-ва. Правила вычисления.
- •2.Определители 3-го порядка. Методы вычисления.
- •3.Системы м линейных n неизвестных. Основные понятия и решения.
- •4.Определение матрицы. Классификация матриц. Действия над ними.
- •5.Определение обратной матрицы, ее св-ва. Вычисление обратной матрицы.
- •6.Ранг матрицы
- •8.Понятие о линейной зависимости и независимости (векторов).
- •9.Теорема о ранге матрицы, ее следствие.
- •10.Вычисление обратной матрицы с помощью элементарных преобразований.
- •11.Теорема Кронекера Капелли. (о совместности решения сист.)
- •12.Однородные сист. Линейных ур-й. Их св-ва.
- •13.Метод Гаусса. Решение сист. Линейных алгебраических ур-й этим методом.
- •14.Векторы. Основные определения.
- •15.Линейные операции над векторами.
- •16.Определение проекция вектора.
- •17.Теоремы о проекциях векторов.
- •18.Скалярное произведение векторов. Его св-ва.
- •19.Длина вектора, расстояние между точками.
- •20.Угол между двумя векторами. Направление косинуса (cos) вектора.
- •21.Условие параллельности и перпендикулярности векторов.
- •22.Деление отрезка в данном отношении.
- •23.Векторное произведение векторов. Его св-ва.
- •24.Выражение векторного произведения через проекции векторов.
- •25.Смешанное произведение векторов и его св-ва.
- •26.Объем параллелепипеда и пирамиды с помощью смешанного произведения векторов.
- •27.Прямая линия на плоскости.
- •28.Исследование общего ур-я прямой.
- •30.Угол между двумя прямыми.
- •32.Расстояние от точки до прямой.
- •34.Исследование общего ур-я плоскости.
- •36.Условие параллельности и перпендикулярности плоскостей.
- •37.Расстояние от точки до плоскости
- •38.Прямая в пространстве
- •39.Угол между двумя прямыми в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
- •40.Угол между прямой и плоскостью
- •41.Условие перпендикулярности и параллельности прямой и плоскости.
- •42.Вывод ур-й кривых 2-го порядка. (окружность, эллипс, гипербола, парабола)
- •42.Поверхности 2-го порядка
- •45.Модуль действительного числа. Его св-ва.
- •46. Числовая последовательность. Предел числовой последовательности.
- •48.Бесконечно малые и бесконечно большие ф-и и их св-ва.
- •49.Основные теоремы о пределах: предел суммы, разности, произведения, частного
- •50.Замечательные пределы
- •51.Сравнение бесконечно малых. Теоремы об эквивалентных бесконечно малых(табл.).
- •52. Определение непрерывности ф-и в точке. Классификация точек разрыва.
- •55.Понятие производной. Геометрический и физический смысл производной.
- •Геометрический смысл производной.
- •3. Физический смысл производной.
- •56.Необходимые условия существования производной.
- •57.Вывод формулы производной от элементарных ф-й.(в тетради)
- •58.Дифференцирование ф-й заданных неявно и параметрически.
- •21.2. Функция, заданная параметрически
- •59.Дифференциал ф-и. Ее геометрический смысл. Св-ва. Таблица дифференциалов.
- •Свойства дифференциала аналогичны свойствам производной.
- •60.Производная и дифференциал высших порядков.
- •61.Формула приближенного вычисления ф-и.
- •62.Теоремы о среднем: Ферма, Ролля, Лагранжа, Каши.
- •3. Теорема Коши
- •64.Выпуклость, вогнутость, точки перегиба графика.
- •65.Асимптоты графика ф-и.
- •66.Общая схема исследования ф-и и построение графика.
42.Поверхности 2-го порядка
Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:
![]() -
(12.1)
-
(12.1)
уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
Если
найти собственные числа и нормированные
собственные векторы матрицы квадратичной
формы
![]() и перейти к системе координат, определяемой
базисом из ортонормированных собственных
векторов, уравнение (12.1) можно привести
к одному из следующих видов:
и перейти к системе координат, определяемой
базисом из ортонормированных собственных
векторов, уравнение (12.1) можно привести
к одному из следующих видов:
эллипсоидом
называется поверхность, которая в
некоторой прямоугольной системе
координат определяется уравнением
:
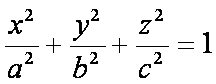 (1)
Уравнение (1) называется
каноническим
уравнением эллипсоида.
Установим геометрический
вид эллипсоида. Для этого рассмотрим
сечения данного эллипсоида плоскостями,
параллельными плоскости Oxy.
Каждая из таких плоскостей определяется
уравнением вида z=h,
где h
–
любое число, а линия, которая получается
в сечении, определяется двумя
уравнениями
(1)
Уравнение (1) называется
каноническим
уравнением эллипсоида.
Установим геометрический
вид эллипсоида. Для этого рассмотрим
сечения данного эллипсоида плоскостями,
параллельными плоскости Oxy.
Каждая из таких плоскостей определяется
уравнением вида z=h,
где h
–
любое число, а линия, которая получается
в сечении, определяется двумя
уравнениями
 (2)
Исследуем уравнения (2) при
различных значениях h.
1)
Если
(2)
Исследуем уравнения (2) при
различных значениях h.
1)
Если
![]() >
c
(c>0),
то
>
c
(c>0),
то
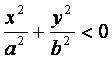 и
уравнения (2) определяют мнимый эллипс,
т. е. точек пересечения плоскости z=h
с
данным эллипсоидом не существует.
2)
Если
и
уравнения (2) определяют мнимый эллипс,
т. е. точек пересечения плоскости z=h
с
данным эллипсоидом не существует.
2)
Если
![]() ,
то
,
то
![]() и
линия (2) вырождается в точки (0; 0; + c)
и (0; 0; - c)
(плоскости
и
линия (2) вырождается в точки (0; 0; + c)
и (0; 0; - c)
(плоскости
![]() касаются
эллипсоида).
3) Если
касаются
эллипсоида).
3) Если
![]() ,
то уравнения (2) можно представить в
виде
,
то уравнения (2) можно представить в
виде
 откуда
следует, что плоскость z=h
пересекает
эллипсоид по эллипсу с полуосями
откуда
следует, что плоскость z=h
пересекает
эллипсоид по эллипсу с полуосями
![]() и
и
![]() .
При уменьшении
.
При уменьшении
![]() значения
значения
![]() и
и
![]() увеличиваются
и достигают своих наибольших значений
при
увеличиваются
и достигают своих наибольших значений
при
![]() ,
т. е. в сечении эллипсоида координатной
плоскостью Oxy
получается
самый большой эллипс с полуосями
,
т. е. в сечении эллипсоида координатной
плоскостью Oxy
получается
самый большой эллипс с полуосями
![]() и
и
![]() .
Аналогичная
картина получается и при пересечении
данной поверхности плоскостями,
параллельными координатным плоскостям
Oxz
и
Oyz.
Таким
образом, рассмотренные сечения позволяют
изобразить эллипсоид как замкнутую
овальную поверхность (рис. 156). Величины
a,
b, c называются
полуосямиэллипсоида.
В случае a=b=c
эллипсоид
является сферой.
.
Аналогичная
картина получается и при пересечении
данной поверхности плоскостями,
параллельными координатным плоскостям
Oxz
и
Oyz.
Таким
образом, рассмотренные сечения позволяют
изобразить эллипсоид как замкнутую
овальную поверхность (рис. 156). Величины
a,
b, c называются
полуосямиэллипсоида.
В случае a=b=c
эллипсоид
является сферой.
Однополостный гиперболоид (рис. 4.20)
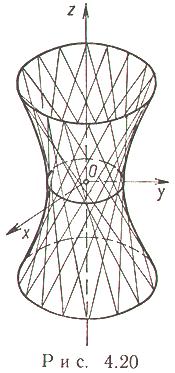
Каноническое уравнение:
![]()
a = b - однополостный гиперболоид вращения вокруг оси Oz.
Горловой
эллипс:
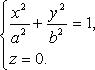
Асимптотический
конус:
![]()
Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).
Двуполостный гиперболоид (рис. 4.21)
Каноническое уравнение:
![]()
a = b - двуполостный гиперболоид вращения вокруг оси Oz.
Асимптотический конус:
![]()
Сечения
двуполостного гиперболоида плоскостями:
либо эллипс, либо гипербола, либо
парабола, либо точка, либо
![]() .
.
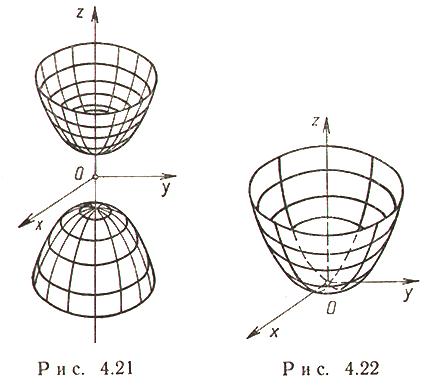
Эллиптический параболоид (рис. 4.22)
Каноническое уравнение:
![]()
p = q - параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .
![]()
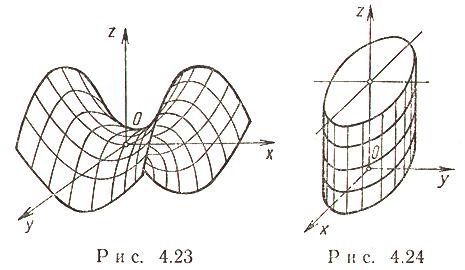
Гиперболический параболоид (рис. 4.23)
Каноническое уравнение:
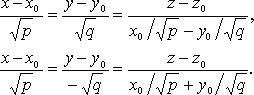
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через
каждую точку
![]() проходят
две прямолинейные образующие:
проходят
две прямолинейные образующие:
![]()
Эллиптический цилиндр (рис. 4.24)
Каноническое уравнение:
![]()
при a = b - круговой цилиндр.
Г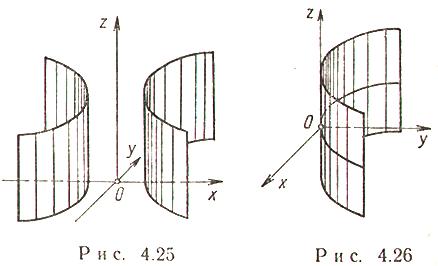 иперболический
цилиндр (рис. 4.25)
иперболический
цилиндр (рис. 4.25)
Каноническое уравнение:
Параболический цилиндр (рис. 4.26)
Каноническое уравнение:
![]()
определяет одну из следующих поверхностей:

