27.Прямая линия на плоскости.

В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y)=0. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:

28.Исследование общего ур-я прямой.

Общее уравнение

Ax + By + C ( > 0).

     Вектор = (А; В) - нормальный вектор прямой.

      В векторном виде: + С = 0, где - радиус-вектор произвольной точки на прямой (рис. 4.11).

     Частные случаи:

     1) By + C = 0 - прямая параллельна оси Ox;

     2) Ax + C = 0 - прямая параллельна оси Oy;

     3) Ax + By = 0 - прямая проходит через начало координат;

     4) y = 0 - ось Ox;

     5) x = 0 - ось Oy.

29.Ур-е в различных формах: через две точки, ур-е в отрезках, каноническое ур-е, ур-е через точку и известный угловой коэффициент, нормальное ур-е прямой.

     Уравнение прямой в отрезках

где a, b - величины отрезков, отсекаемых прямой на осях координат.

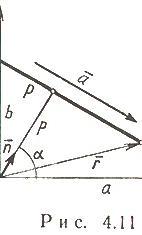
     Нормальное уравнение прямой (рис. 4.11)

где - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Векторно-параметрическое уравнение прямой

где - фиксированная точка, лежащая на прямой; - направляющий вектор (см. рис. 4.11).

     В координатах (параметрические уравнения):

     Каноническое уравнение прямой

     Уравнение прямой по двум точкам (рис. 4.12)

или

или

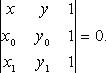
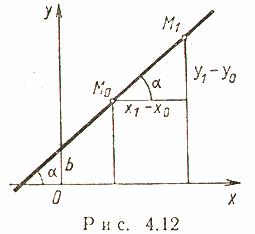     Уравнение прямой по точке и угловому коэффициенту (рис. 4.12)

или

где b - величина отрезка, отсекаемого прямой на оси Oy.

30.Угол между двумя прямыми.

пусть заданы две пересекающиеся линии и не парал. Осям координат.

 

 

 

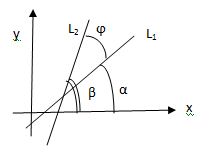
 За угол между прямыми принимают острый угол.

tgα=k₁, tgβ=k₂,  ϕ=β-α,

угол между прямыми это угол на который нужно повернуть L1 до совпадения с одним из направления L2 (этот угол не еденственен).

 Угол между двумя прямыми: 

 

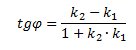
Если прямые параллельны, то k₁=k₂ и  b₁≠b₂

Если прямые перпендикулярны, то k₁*k₂=-1

Если прямые пересекаются, то k₁≠k₂

Если прямые совпадают, то k₁=k₂ и  b₁=b₂ 

31.Ур-е параллельности и перпендикулярности двух прямых.

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     

б) Для случая, когда прямые заданы уравнениями в общем виде , необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     

  Это условие может быть записано также в виде

k₁k₂ = -1.     (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.     (12)