1.Определите 2-го порядка. Их св-ва. Правила вычисления.

Будем рассматривать квадратные матрицы

Определители являются основными числовыми характеристиками квадратных матриц.

 Определителем (детерминантом) матрицы ,

 состоящей из одного числа   , называется само это число.

Определителем матрицы А=  второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

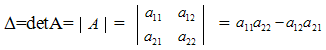
Св-ва определителей:

1. Величина определителя не измениться при транспонировании

2. При перестановке в определителе двух строк(столбцов) величина определите меняется на противоположное

3. Если в определителе сущ. Две одинаковых строки(столбца), то он =0.

4. Если в определителе есть общий множитель в строке(столбце) то он выноситься за знак определителя.

5. Если в определителе сущ. строка (столбец), состоящая из нулей, то величина определителя =0.

6. Если в определителе сущ. пропорциональные строки (столбцы), то определитель =0

7. Если в определителе каждый элемент строки (столбца) представляет сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей.

8. Величина определителя не измениться если к элементам некоторой строки (столбца) прибавить элемент другой строки (столбца), умноженное на одно и то же число отличное от нуля.

9. Величина любого определителя равна сумме произведения элементов какой-либо другой строки (столбца), умноженное на их алгебраические дополнения.

10. Величина опр. Всегда = 0, если берется сумма произведений элементов столбца(строки) и умножается на алг. дополнения другого столбца(строки).

2.Определители 3-го порядка. Методы вычисления.

Миноры и алгебраические дополнения

Если D = |A| - определитель порядка n, то минором M_ij элемента а_ij называют определитель порядка n-1, получающийся из D вычеркиванием i-й строки и j-го столбца. Под алгебраическим дополнением A_ij элемента а_ij понимают минор M_ij, домноженный на (-1)^i+j, т.е. A_ij = (-1)^i+jM_ij Например для определителя 3-го порядка:

D =

a11 a12 a13 a21 a22 a23 a31 a32 a32

Минор элемента а23 будет M23 =

a11 a12 a31 a32

Алгебраическим дополнением элемента а₂₃ будет A₂₃= (-1)²⁺³M₂₃= (-1)⁵M₂₃= -M₂₃ а для элемента а₁₃ , A₁₃= M₁₃ и т.п.

Теорема разложения

Если D = |A| - определитель n-го порядка, то

D =

n Σ i=1

aikAik

=

n Σ i=1

akiAki

n Σ i=1

aikAim

=

n Σ i=1

akiAmi = 0,  для k неравного m

т.е. сумма произведений всех элементов какой-либо строки (или столбца) на соответствующие алгебраические дополнения равна значению определителя. Сумма произведений всех элементов какой-либо строки (или столбца) на алгебраические дополнения соответствующих элементов другой строки (или другого столбца) равна нулю:

Вычисление определителей

Значение определителя 2-го порядка легко вычисляется по определению используя формулу (2). Для нахождения значения определителя 3-го порядка можно использовать формулу (3). Определители более высоких порядков в принципе тоже можно было бы вычислять по определению, однако это требует очень больших усилий. Чаще поступают следующим образом: определитель n-го порядка сводят к опреде-лителям (n-1)-го порядка, последние - к определителям (n-2)-го порядка и т. д., до тех пор, пока, наконец, не получат определители 3-го или 2-го порядка. В основе этого принципа "постепенного понижения порядка" лежит теорема разложения: определитель n-го порядка D записывается в виде суммы определителей порядка (n-1) ("раскладывается по элементам i-й строки или j-го столбца"); к каждому из этих определителей порядка n-1 вновь может быть применена теорема разложения. Если все элементы а_ik i-й строки определителя D, кроме одного, равны нулю, то сумма, полученная после применения теоремы разложения, содержит только одно отличное от нуля слагаемое. Таким образом, вычисления существенно упрощаются, если перед разложением определителя по элементам i-й строки как можно больше из них будут превращены в нули. Это становится возможным благодаря применению свойств определителей (особенно свойства 5). Еще удобнее оказывается вычисление определителя, если, применяя его свойства, можно преобразовать его так, чтобы все элементы, стоящие слева и ниже диагонали а₁₁ , а₂₂, ..., а_nn были равны нулю. Как легко понять на основании теоремы разложения, значение определителя получается тогда просто как произведение членов, стоящих на главной диагонали:   D = a₁₁a₂₂.. .а_nn .

Рассмотрим матрицу третьего порядка:

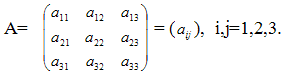
Определителем матрицы A третьего порядка называется число