
4. Число сочетаний.
Предположим, что по n ячейкам размещается r неразличимых между собой (в каждую ячейку можно поместить только один предмет). Тогда число различных размещений совпадает с числом различных групп по r ячеек и равно
 .
.
Вышеприведенная формула также определяет число подмножеств размерности r множества из n элементов, где два подмножества считаются различными, если они отличаются элементами, а порядок их следования – несущественен. Соответственно в знаменателе имеем деление на r!.
Полученная формула относится также к разбиению n различных элементов (ячеек) на две группы (группа 1 - пустые ячейки и группа 2 - занятые ячейки).
Результат разбиения можно представить в виде вектора размерности n, содержащего r единиц (признак незанятости ячейки) и (n-r) двоек (признак занятости ячейки). Два разбиения различны, если различны соответствующие им вектора.
Рассмотрим
общий случай разбиения n
различных элементов на k
групп, причем в группе с номером i
число элементов равно ni
и
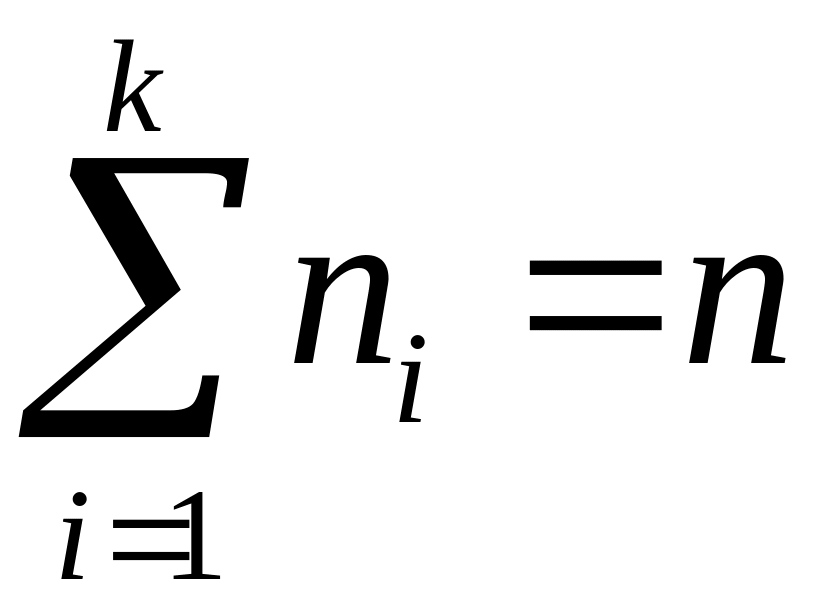 .
Результат разбиения вновь можно
представить в виде вектора размерности
n,
содержащего n1
единиц, n2
двоек, …, nk
чисел k.
Два разбиения различны, если различны
соответствующие им вектора. Число
различных разбиений дается формулой
.
Результат разбиения вновь можно
представить в виде вектора размерности
n,
содержащего n1
единиц, n2
двоек, …, nk
чисел k.
Два разбиения различны, если различны
соответствующие им вектора. Число
различных разбиений дается формулой
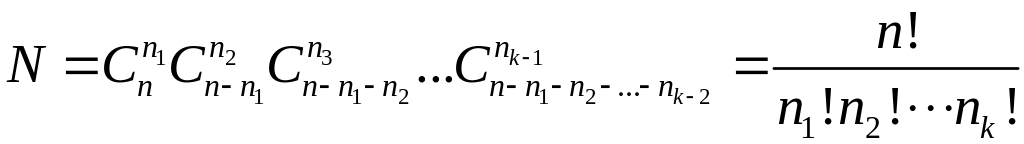 .
.
Пример 1: N различных шаров случайно размещаются по М ящикам, М>N.
Найти вероятность, что все шары попадут в разные ящики.
Решение.
Число способов размещения N шаров по М ящикам равно МN.
Число способов размещения N шаров по М ящикам, когда в каждый ящик попадает по одному шару равно
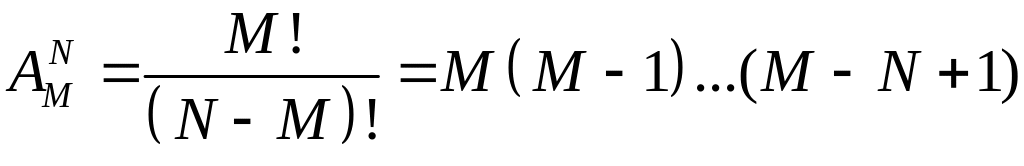 .
.
Ответ:

Пример 2: (гипергеометрическое распределение вероятностей).
Существует большой класс задач ТВ, которые можно интерпретировать в рамках так называемой урновой схемы: событие, вероятность которого надо вычислить, можно трактовать как выбор шаров различной расцветки из урны. Простейшая из таких схем состоит в следующем. Из урны, содержащей М черных и N-M белых шаров, случайно вынимается n шаров. Какова вероятность того, что выборка содержит m черных шаров?
Решение.
В
этом эксперименте пр-во элементарных
событий состоит из
![]() исходов. Решение задачи сводится к
подсчету числа выборок из n
шаров, которые содержат m
черных и n-m
белых шаров.
исходов. Решение задачи сводится к
подсчету числа выборок из n
шаров, которые содержат m
черных и n-m
белых шаров.
Очевидно
что,
![]() .
.
Правая часть неравенства означает, что число черных шаров m должно быть меньше объема выборки n и числа M черных шаров.
Левая часть неравенства означает, что если объем выборки n превышает число белых шаров N-M, то число черных шаров не может быть меньше, чем n-(N-M) = (размер выборки – число белых шаров).
Число
способов выбора из М
черных шаров m
шаров равно
![]() .
Число способов выбора из N-M
белых шаров n-m
шаров равно
.
Число способов выбора из N-M
белых шаров n-m
шаров равно
![]() .
.
Следовательно общее число исходов, соответствующее событию А – «выборка содержит m черных шаров» равно , и искомая вероятность Р(А)= / .
Пример3: (Задача про рыб).
Из озера вылавливается 1000 рыб. Каждая из рыб метится красной меткой и отпускается в озеро. При следующем улове среди 1000 рыб оказалось 100 меченых. Какие выводы можно сделать относительно числа рыб?
Решение.
Пусть n – (неизвестное) число рыб в озере, n1-число меченых рыб (n1=1000), r – число рыб, пойманных при втором улове (r=1000), k- число меченых рыб, пойманных при втором улове (k =100).
Вероятность поймать k меченых рыб есть
 .
.
Для
оценки числа рыб n
предлагается найти n
из условия максимума вероятности
![]() ,
то есть в предположении, что при втором
улове реализовалось наиболее вероятное
событие. Основной довод в пользу такой
оценки числа рыб состоит в простом
житейском наблюдении: если происходит
какое-либо событие, то это событие должно
иметь наибольшую вероятность среди
всех остальных исходов.
,
то есть в предположении, что при втором
улове реализовалось наиболее вероятное
событие. Основной довод в пользу такой
оценки числа рыб состоит в простом
житейском наблюдении: если происходит
какое-либо событие, то это событие должно
иметь наибольшую вероятность среди
всех остальных исходов.
Для определения максимума вероятности по переменной n, рассмотрим
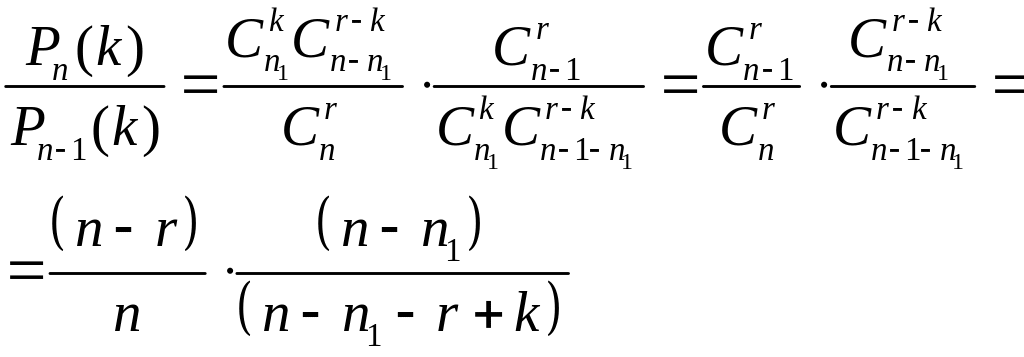
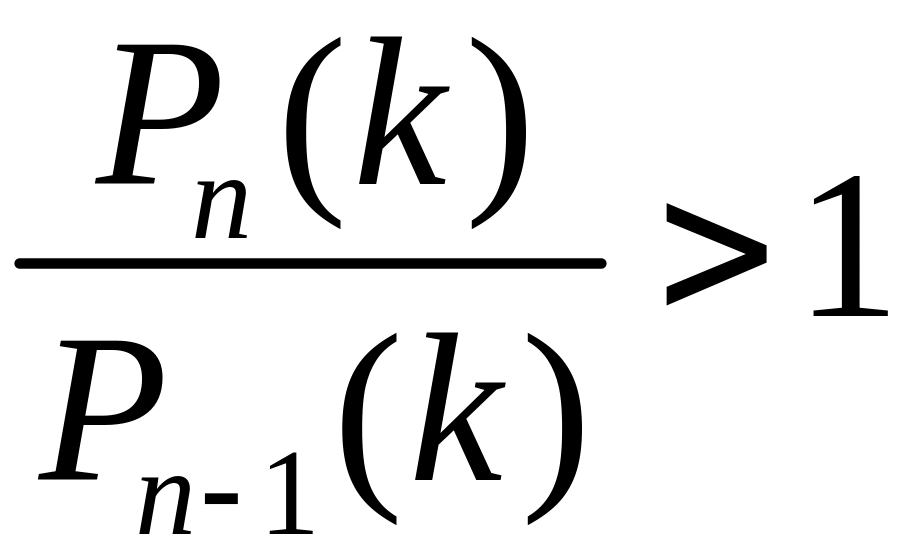 при
при
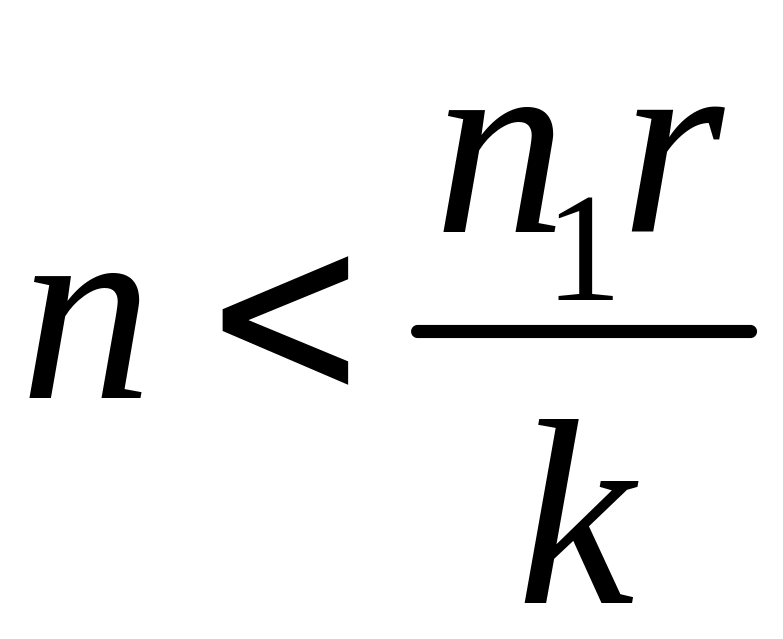 и
и
 при
при
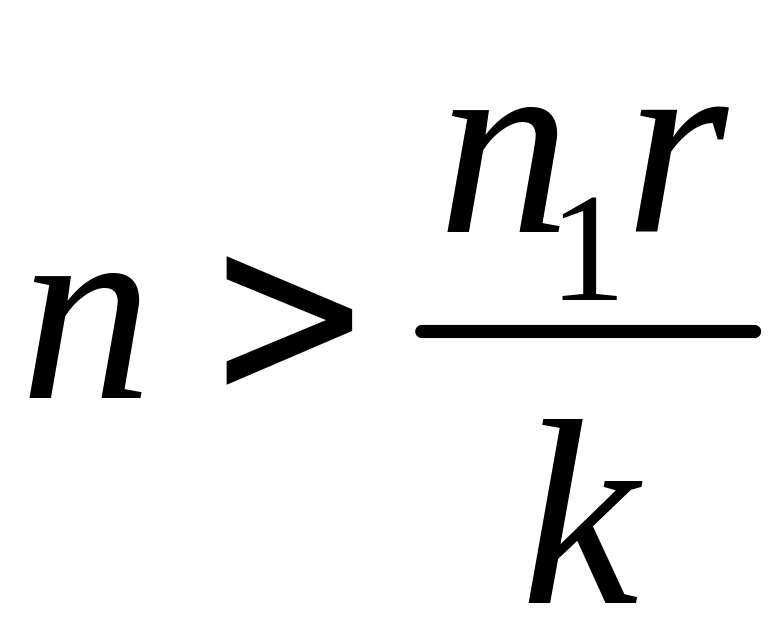 .Это
значит, что при возрастании n
вероятности
сначала возрастают, а затем убывают.
Максимум достигается, когда n
есть максимальное целое число, не большее
чем
.Это
значит, что при возрастании n
вероятности
сначала возрастают, а затем убывают.
Максимум достигается, когда n
есть максимальное целое число, не большее
чем
![]() .
.
Геометрические вероятности.
Еще в самом начале развития теории вероятностей была замечена недостаточность классического определения вероятности, основанного на конечности множества элементарных исходов. В результате было построено понятие вероятности когда имеется бесконечное число равновероятных исходов.
Пусть
элементарные исходы можно представить
точками n-мерного
евклидового пространства, равномерно
заполняющими некоторую область G.
Тогда событиям будут соответствовать
подобласти области G.
За вероятность события А принимается
отношение площади (объема) области А к
площади (объему)
![]() :
:
![]() .
.
Пример 4: (Задача о встрече). Двое договорились встретиться в промежутке между 10 и 11 часами, причем каждый ждет другого в течение 15 минут и потом уходит. Считая, что у каждого все моменты прихода на место встречи с 10 до 11 равновозможные, найти вероятность их встречи.
Решение.
Представим элементарные события в виде пар чисел (x,y), где x – время прихода одного из них, а y - время прихода другого. Из условия задачи элементарные события равномерно заполняют квадрат со стороной, равной единице (в часах).
Встреча
происходит, если
![]() .
.
Вероятность
встречи определяется отношением площадей
![]() .
.
Некоторые свойства вероятности.
Во всех трех рассмотренных случаях вероятность удовлетворяет следующим очевидным свойствам.
1.
![]()
2.![]()
3.
Если
(события А и В несовместны), то
![]() .
.
Дальнейшее построение теории будет проведено так, что эти интуитивно понятные свойства будут сохраняться.
