Работа, совершаемая при перемещении контура с током в магнитном поле.

Рассмотрим отрезок проводника с током, способный свободно перемещаться по двум направляющим во внешнем магнитном поле (рис.9.5). Магнитное поле будем считать однородным и направленным под углом α по отношению к нормали к плоскости переме-щения проводника.

 

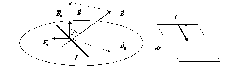
Рис.9.5. Отрезок проводника с током в однородном магнитном поле.

Как видно из рис.9.5, вектор   имеет две составляющие   и  , из которых только составляющая  создает силу, действующую в плоскости перемещения проводника. По абсолютной величине эта сила равна:

,

где I – сила тока в проводнике; l – длина проводника; B – индукция магнитного поля.

Работа этой силы на элементарном пути перемещения ds есть:

.

Произведение lds равно площади dS, заметанной проводником при движении, а величинаBdScosα равна потоку магнитной индукции dФ через эту площадь. Следовательно, можем написать:

dA=IdФ.

Рассматривая отрезок проводника с током как часть замкнутого контура и интегрируя это соотношение, найдем работу при перемещении контура с током в магнитном поле:

A = I(Ф₂ – Ф₁)

где Ф₁ и Ф₂ обозначают поток индукции магнитного поля через площадь контура соответственно в начальном и конечном положениях.

40.

Движение заряженных частиц

в

Однородном магнитном поле

Рассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0.

Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения. Прежде всего, отметим, что действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца

остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием

откуда

Если энергия электрона выражена в эВ и равна U, то

 (3.6)

и поэтому

Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен

Подставляя сюда вместо r его выражение по формуле (3.6), имеем:

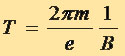(3.7)

Частота же оказывается равной

Для данного типа частиц и период, и частота зависят только от индукции магнитного поля.

Выше мы предполагали, что направление начальной скорости перпендикулярно к направлению магнитного поля. Нетрудно сообразить, какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля.  В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью

В результате сложения обоих движений частица будет двигаться по цилиндрической спирали.

Шаг винта этой спирали равен

подставляя вместо T его выражение (3.7), имеем:

41.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота. Свойства

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле   течёт электрический ток под действиемнапряжённости  . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов   не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов   можно выразить через плотность тока:

где   — концентрация носителей заряда. Тогда

Коэффициент   пропорциональности между   и   называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак  , что объясняется в полуклассической и квантовой теориях твёрдого тела.

42.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Майклом Фарадеем 29 августа^{[источник не указан 111 дней]} 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

43.