6.Формула Тейлора с остаточным членом Лагранжа. Формула Маклорена.

1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но хǂа. Тогда между точками х и а найдется такая точка e, что справедлива формула:

 

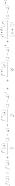
называется остаточным членом в форме Лагранжа.

2) Формулой Маклорена называется  формула Тейлора при а = 0:

7.Экстремум

Экстремум — максимальное или минимальное значение функции на заданном множестве.

Необходимое условие существования экстремума:

если непрерывная функция имеет экстремум в точке х₀, то ее производная в этой точке равна нулю или не существует.

Доказательство.

Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x₀+ Δx)<f(x₀), т.е. Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0–0

f'(x₀) ≥ 0 а при Δx → 0+0

f'(x₀) ≤ 0. Так как f'(x₀) определяет число, то эти два неравенства совместны только в том случае, когда

f'(x₀) = 0.

8.Асимптоты

Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.

Виды асимптот:

1) Вертикальная:

Вертикальная асимптота — прямая вида при условии существования предела .

2) Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела .

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов