3.Производная сложной функции, обратной, параметрически заданной

1) Пусть дана функция y=f(u), где u=g(х), тогда имеет место сложная функция y= f(g (х)), при чём множество значений u входит во множество значений f. Если функция φ(х) имеет производную u, то сложная функция y= f(g(х)) имеет производную в точке х, и имеет место формула:

Доказательство:

= *

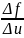Перейдём к пределу при ->0, тогда тоже стремится к 0, потому что u(х) непрерывна. Получаем y^|(x)=y^|(u)*u^|(x)

2) Если для функции y=f(х) существует обратная функция х=g(y), которая в некоторой точке y₀ имеет производную конечную, отличную от 0, то в соответствующей точке х₀=g(х₀) функция y=f(х) имеет производную f^|(х₀), равную и справедлива формула f^|(х) = .

Доказательство:

Так как х=g(y) дифференцируемая в точке , то х=g(y) непрерывна в этой точке, по этому функция y=f(х) непрерывна в точке х₀=g( ).

= . Пусть ->0, тогда ->0.

Перейдём к пределу в последнем выражении при ->0:

=

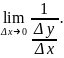
x_y^| = => y_x^| =

3) Если х=φ(t), y=ψ(t) tє(a;b) и существует обратная функция t=θ(х) для х= φ(t), то говорят о параметрическом задании функции y=ψ(θ(х)).

Пусть х=φ(t), y=ψ(t) определены и дифференцируемы при tє(a;b), при чём x_t^|= φ^|(t)ǂ0 и х=φ(t) имеет обратную функцию t=θ(х)

y=ψ(t)= ψ(θ(х))

y_x^|=(ψ(θ(х)))^|= ψ^|(θ(х))* θ^|(х)

Так как t=θ(х) и х=φ(t) обратные функции, то по формуле производной обратной функции θ^|(х) = ,

Поэтому y_x^|=(ψ(θ(х)))^|= ψ^|(θ(х))* θ^|(х)=

4.Дифференциал функции в точке

Функция f(x)называется дифференцируемой в точке х₀, если её приращение представлено в виде:

Δf=f(x₀+Δx)- f(x₀)=A* Δx+O(Δx)

А-число не зависящее от Δx;

O(Δx)-функция более высокого порядка малости, чем Δx при Δx->0.

Дифференциал функции в точке х₀ – это линейная часть приращения дифференцируемой функции:

Δ(х₀)= A*Δx

Свойства дифференциала:

1) dC=0, C=const

2) d(u+v)=du+dv

3) d(u*v)=udv+vdu

4) d( ) =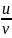

5) инвариантность формы записи дифференциала:

Пусть y=f(x), x- независимая переменная

dy=f^|(x)dx

y=f(x), x= φ(t), при чём множество значений f(x) входит в ОДЗ y. Тогда имеет место суперпозиция: y=f[φ(t)], y зависит от x, а x от t.

x промежуточная переменная, а tнезависимая. Если функция φ(t) имеет производную в точке t, а функция f(x) имеет производную в соответствующей точке х, тогда сложная функция имеет дифференциал равный:

dy=f_x^|[φ(t)]*x_t^|dt=f_x^|(x)*dx (1)

dy= f_x^|(x)*dx (2)

Форма записи дифференциала не меняется, то есть она не зависит от того является ли х независимой переменной (1) или зависимой (2).

5.Теоремы о среднем

1) Теорема Ферма:

Если функция f имеет производную в точке c и достигает в этой точке локального экстремума, то .

2) Теорема Ролля:

Если функция y=f(x) непрерывна на [a,b], дифференцируема на (a,b) и f(a)=f(b), то существует точка cє(a,b), такая, что .

3) Теорема Коши:

Если функции f(x) и g(x) непрерывны на [a,b] и дифференцируемы на (a,b), и  в (a,b), то существует точка cє(a,b) такая, что

4) Теорема Лагранжа:

Пусть: 1) f(x) определенна и непрерывна в замкнутом промежутке [a,b]; 2) существует конечная производная f^|(x), по крайней мере, в открытом промежутке (a,b). Тогда между a и b найдётся такая точка с (a<c<b), что для неё выполняется равенство

Доказательство:

Введём вспомогательную функцию F(x) в [a,b]

F(x)=f(x)-f(a)-

Эта функция 1) непрерывна на [a,b]; 2) В (a,b) имеет определённую конечную производную

F^|(x)=f^|(x)- ;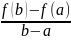

3) F(a)=F(b)=0, F(x) принимает равные значения на концах промежутка. Тогда по теореме Ролля между a и b найдётся такая точка, что F^|(с)=0.

f^|(с)- , откуда f^|(с)= или f(b)-f(a)= f^|(с)(b-a).