11) Свойства непрерывных функций на замкнутом промежутке
Теорема Больцано — Коши: Пусть функция f (x) определена и непрерывна в замкнутом промежутке [a, b] и на концах этого промежутка принимает значения разных знаков. Тогда между a и b необходимо найдется такая точка c, в которой функция обращается в нуль.
Доказательство:
Для
определенности положим, что
.
Разделим промежуток [a,
b] пополам точкой
.
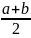Если функция f (x) обратится в
нуль в этой точке, то теорема доказана.
Пусть
.
Тогда на концах одного из промежутков
,
функция
будет принимать значения разных знаков
(отрицательное на левом конце и
положительное — на правом). Обозначив
этот промежуток через
,
имеем
Разделим
пополам промежуток
и снова отбросим тот случай, когда f
(x) обращается в нуль в середине
этого промежутка.
Обозначим
через
ту из половин промежутка, для которой
Продолжим
процесс построения промежутков. При
этом мы либо после конечного числа
шагов получим точку, где функция
обращается в нуль, — и доказательство
теоремы завершится, — либо получим
бесконечную последовательность
вложенных один в другой промежутков.
В этом случае для n-го
промежутка
будем
иметь
причем длина его, очевидно, равна
Если
в качестве последовательности
возьмем
последовательность (an)
левых концов построенных отрезков, а
в качестве последовательности (yn)
— последовательность (bn)
правых их концов, то по лемме о вложенных
промежутках получим, что существует
точка
,
для которой
Покажем, что эта точка удовлетворяет требованиям теоремы.
Переходя к пределу в неравенствах и используя при этом непрерывность функции (в частности, в точке x=c), получим, что одновременно
так
что, действительно,
.
Теорема Вейерштрасса.
Пусть
функция f(x) определена и непрерывна на
замкнутом отрезке [a, b]. Тогда она
ограничена на этом отрезке, т.е. существуют
такие числа m и M, что
x
принадлежащего [a,b] f(x) больше либо равно
m и меньше либо равно M.
1.Производная функции в точке
Производной функции f(x) в точке х называется предел отношения приращения функции к приращению аргумента при стремлении последнего к 0, если этот предел существует и конечный.
Геометрический смысл производной:
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Необходимое условие существования производной: Если функция f(x) имеет производную в точке х, то она непрерывна в этой точке.
Доказательство:
По
определению производной существует
конечный предел
.
Тогда
А это означает, что функция f(x) непрерывна в точке х0.
Уравнение касательной:
y(х) = f(х0) + f '(х0)(x – х0)
Уравнение нормали:
2.Производная(+;-;*;/)
1)
Воспользуемся
определением производной и свойством
предела непрерывной функции.
2)
.
Запишем
предел отношения приращения произведения
функций к приращению аргумента. Будем
учитывать, что
и
Что и требовалось доказать.
3)
.
Стоит оговориться, что g(x) не
обращается в ноль ни при каких x из
промежутка X.
По
определению производной
