1.Абсолютная величина действительного числа Абсолютной величиной (или модулем) действительного числа а называется неотрицательное число |а|, определяемое соотношением |а|={а, а>=0; -a, a<0. Свойства: 1) Модуль любого действительного числа а, есть неотрицательное число: |а|>=0;
2) Каждое действительное число а не больше своего модуля и не меньше числа противоположного модулю: -|а|<=а<=|а|; 3) Модуль суммы двух или более слагаемых не больше суммы модулей этих чисел: |а+b|<=|а|+|b|
-|а|<=а<=|а|; -|b|<=b<=|b|; -(|а|+|b|)<=а+b<=|а|+|b|; |а+b|<=|а|+|b|; 4) Модуль разности двух чисел не меньше разности модулей этих чисел:
|а-b|>=|а|-|b| |а|=|(а-b)+b|<=|а-b|+|b|; |а-b|>=|а|-|b|; 5) Модуль произведения двух или более множителей равен произведению модулей этих чисел: |а*b|=|а|*|b|; 6) Модуль частного двух чисел равен частному модулей этих чисел: |а/b|=|а|/|b|;
7) Сумма модулей числа нулю тогда и только тогда, когда каждое число равно нулю.
8) Модуль разности модулей двух чисел не больше модуля разности этих чисел:
||а|-|b||<=|а-b|
|а|-|b|<=|а-b|;
|b|-|а|<=|b-а|=|а-b|;
|а|-|b|<=|а-b|;
-(|а|-|b|)<=|а|-|b|;||а|-|b||<=|а-b|
9)
Квадратный
корень квадрата числа равен модулю
этого числа:
=|а|;
2.Числовая последовательность
Числовая
последовательность-множество
значений упорядоченное наподобие
натурального ряда чисел по возрастанию
номеров; записывается в виде {
}=
.
Отдельные числа последовательности { } называют её элементами.
Постоянное число а называется пределом последовательности (переменной) , если для любого сколь угодно малого наперёд заданного числа ε>0 найдётся такой номер N, что как только n>N выполняется неравенство | -a|<ε.
Геометрическое определение предела: Постоянное число а называется пределом переменной , если для любой ε-окрестности точки а найдётся такой номер N, что начиная с этого номера все значения переменной попадают в ε-окрестность.
Основные теоремы:
1) Если переменная ->a, а a>p (a<q), то начиная с некоторого номера, то >p ( <q). В частности p=q.
2) Теорема о единственности предела: Переменная не может одновременно стремится к двум различным пределам.
Доказательство:
Пусть ->a и ->b (aǂb)
Пусть
r-некоторое
число. Так как
->a,
но a<r,
то начиная с некоторого номера
,
n>
,
<r.
Так как
->b,
а b>r,
для n>
,
>r.
N
наибольшее (из
,
)
->тогда одновременно выполняется 1 и
2.
3) Теорема (об ограниченности переменной имеющей конечный предел): Если переменная имеет конечный предел, то она ограниченна, в том случае, что все её значения содержатся между конечными границами m<= <=M.
Доказательство:
Так как переменная имеет предел, то по определению для любой ε-окрестности (a-ε; a+ε) начиная с некоторого номера все значения попадут в эту ε-окрестность.
Вне
этой окрестности находится конечное
число значений переменной. Так как этих
значений конечное число, то границы
a-ε,
a+ε
можно раздвинуть, взяв в качестве
m-наименьшее
из (
,a-ε),
M-наибольшее
из (
,a-ε).
3. Бесконечно малые переменные
Переменная
называется бесконечно
малой,
если предел
=0.
Переменная есть бесконечно малая, если для любого ε>0 найдётся N такое, что | |<ε (n>N).
Основные свойства:
1)
Сумма
конечного числа бесконечно малых есть
бесконечно малое. Рассмотрим случай
двух слагаемых:
-бесконечно
малое, по определению это значит, что
для любого
>0
найдётся такой
(номер) n>
,
что будет выполняться неравенство
|
|<
.
Так
как
-бесконечно
малое, то по определению для любого ε
в частности
найдётся такой
n>
,
что будет выполняться неравенство
|
|<
.
Возьмём в качестве N> ; N> , тогда неравенства | |< и | |< выполняются одновременно, но сумма | + |<=| |+| |<ε для n>N.
А
это означает по определению, что
величина бесконечно малая.
2) Произведение бесконечно малых на ограниченную переменную есть величина бесконечно малая.
Пусть
-бесконечно
малая, тогда по определению для любого
>0
начиная с некоторого номера N
выполняется неравенство |
|<
.
Пусть -ограниченная переменная, тогда по определению существует число M>0 такое, что <M для всех n.
Тогда | * |<=| |*| |<ε для n>N.
А
это означает по определению, что
произведение
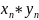бесконечно малое.