Условия перпендикулярности.

Перпендикулярные прямые фигурируют чуть ли не в каждой геометрической задаче. Иногда перпендикулярность прямых известна из условия, а в других случаях перпендикулярность прямых приходится доказывать. Для доказательства перпендикулярности двух прямых достаточно показать, используя любые геометрические методы, что угол между прямыми равен девяноста градусам.

А как ответить на вопрос «перпендикулярны ли прямые», если известны уравнения, задающие эти прямые в прямоугольной системе координат на плоскости или в трехмерном пространстве?

Для этого следует воспользоваться необходимым и достаточным условием перпендикулярности двух прямых. Сформулируем его в виде теоремы.

Теорема.

Для перпендикулярности прямых a и b необходимо и достаточно, чтобы направляющий вектор прямой a был перпендикулярен направляющему вектору прямой b.

Доказательство этого условия перпендикулярности прямых основано на определении направляющего вектора прямой и на определении перпендикулярных прямых.

Добавим конкретики.

Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданы уравнения прямой на плоскости некоторого вида, определяющие прямые a и b. Обозначим направляющие векторы прямых а и b как и соответственно. По уравнениям прямых a и b можно определить координаты направляющих векторов этих прямых – получаем и . Тогда, для перпендикулярности прямых a и b необходимо и достаточно, чтобы выполнялось условие перпендикулярности векторов и , то есть, чтобы скалярное произведение векторов и равнялось нулю: .

Итак, необходимое и достаточное условие перпендикулярности прямых a и b в прямоугольной системе координат Oxy на плоскости имеет вид , где и - направляющие векторы прямых a и b соответственно.

Это условие удобно использовать, когда легко находятся координаты направляющих векторов прямых, а также когда прямым a и b соответствуют канонические уравнения прямой на плоскости или параметрические уравнения прямой на плоскости.

Билет №25. Уравнение плоскости, проходящей через заданную точку и заданным нормальным вектором.

Эту жёсткую конструкцию вектора нормали и точки хорошо знает мишень для игры в дартс. Пожалуйста, вытяните руку вперёд и мысленно выберите произвольную точку пространства, например, маленькую кошечку в серванте. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вашей руке.

Уравнение плоскости, проходящей через точку  перпендикулярно вектору  , выражается формулой:

Выглядит значительно привлекательнее, чем предыдущие мытарства. В некоторых задачах аналитической геометрии уравнение плоскости можно составить несколькими способами, и решение через точку и нормальный вектор – самое оптимальное.

БИЛЕТ №26.

Общее уравнение плоскости в пространстве.

БИЛЕТ №27.

Уравнение плоскости проходящей через три заданные точки.

БИЛЕТ №28.

Уравнение плоскости, отсекающей от координатных осей заданные отрезки.

Если же общее уравнение плоскости является полным

(т.е. ни один из коэффициентов не равен нулю), то его можно преобразовать к виду, называемому уравнением плоскости в отрезках

,

 равны величинам отрез­­ков, отсекаемых плоскостью на координатных осях.

БИЛЕТ №29.

Нормальное уравнение плоскости.

Положение плоскости  вполне определяется заданием единичного вектора , имеющего направление перпендикуляра , опущенного на плоскость из начала координат, и длиной p этого перпендикуляра

Пусть , а  – углы, образованные единичным вектором  с осями  и ;  Возьмем на плоскости произвольную точку  и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости  проекция радиус-вектора  на направление вектора  всегда равно : , т.е.  или  – нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме:

  .

Общее уравнение плоскости  можно привести к нормальному уравнению так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части общего уравнения на нормирующий множитель

 где знак берется противоположным знаку свободного члена  общего уравнения плоскости.

БИЛЕТ №30.

Нахождение расстояния от точки до плоскости.

БИЛЕТ №31.

Нахождение расстояния между параллельными плоскостями.

Расстояние между двумя параллельными плоскостями  выражается формулой:

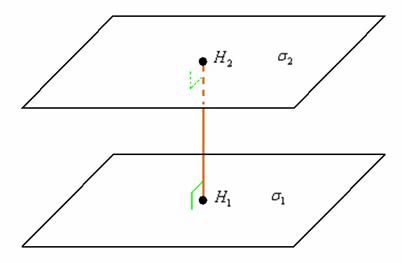
Координаты точек  нам неизвестны, да их и не нужно знать, поскольку перпендикуляр между плоскостями можно протянуть в любом месте.

БИЛЕТ №32.

Нахождение угла между плоскостями.

Две пересекающиеся плоскости  образуют четыре двухгранных угла и любой из этих углов можно считать углом между плоскостями. Иными словами, острый или тупой угол получится – не имеет значения.

Обозначим угол между плоскостями через :

Наклон плоскости однозначно определяется её вектором нормали, поэтому угол между плоскостями равен углу между нормальными векторами данных плоскостей. А угол между векторами рассчитывается с помощью обыденной формулы, рассмотренной на уроке Скалярное произведение векторов:

Распишем формулу в коэффициентах:

БИЛЕТ №33.

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

БИЛЕТ №34.

Общее уравнение прямой в пространстве.

Общее уравнение прямой в пространстве выводится из условия задания прямой, как пересечения двух плоскостей:

БИЛЕТ №35.

Каноническое уравнение прямой.

БИЛЕТ №36.

Параметрическое уравнение прямой в пространстве.

или

(скорее 2)

БИЛЕТ №37.

Уравнение прямой на плоскости, проходящей через заданные две точки.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х2 и х = х 1 , если х 1 = х2 .

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем: