
- •Билет №2. Решение системы линейных алгебраических уравнений методом Жордана Гаусса.
- •Прямой ход метода.
- •Следствие:
- •Замечание:
- •Замечание:
- •Вычисление ранга матриц методом элементарных преобразований.
- •Билет №6. Обратная матрица и метод ее отыскивания.
- •Билет №7. Матричное уравнение и методы его решения.
- •Билет №8. Линейные векторные операции в геометрическом и алгебраическом видах. Векторная алгебра.
- •Билет №15. Общее уравнение прямой.
- •Билет №16. Уравнение прямой на плоскости, отсекающей от координатных осей заданные отрезки.
- •Билет №17. Уравнение прямой на плоскости, проходящей через заданную точку и заданным направляющим вектором.
- •Билет №18. Уравнение прямой на плоскости, проходящей через заданные две точки.
- •Билет №19. Нормальное уравнение прямой на плоскости.
- •Билет №22. Нахождение расстояния между параллельными прямыми на плоскости.
- •Нахождение расстояния между параллельными прямыми – теория, примеры, решения.
- •Условия перпендикулярности.
- •Билет №25. Уравнение плоскости, проходящей через заданную точку и заданным нормальным вектором.
- •Билет №38. Нахождение точки пересечения прямой и плоскости.
- •Билет №39. Нахождение проекции точки на плоскость.
- •Билет №40. Нахождение проекции точки на прямую.
БИЛЕТ №1.
Свойства определителей и применение их для решения системы линейных алгебраических уравнений.
Определители n-ного порядка.
Определитель существует только для квадратной матрицы.
Определитель матрицы – разность произведения элементов.
Определитель матрицы = Детерминант матрицы
Определитель квадратной матрицы – число, которое вычисляется по следующему правилу:

Пример:

Определитель второго порядка.
a11 a12 |
=a11a22 – a12a21 |
A21 a22 |
Определитель третьего порядка. Правило треугольника или Сюрриса.
 (X
перемножаем)
(X
перемножаем)
Минор.
Минором
 квадратной матрицы п-ного
порядка называется определитель
п-1-ого
порядка, полученный из определителя
матрицы А
вычёркиванием i-той строки и j-того
столбца.
квадратной матрицы п-ного
порядка называется определитель
п-1-ого
порядка, полученный из определителя
матрицы А
вычёркиванием i-той строки и j-того
столбца.
Алгебраическое дополнение
Алгебраическим
дополнением
 называется минор этого элемента, взятый
с определённым знаком, который определяется
по формуле:
называется минор этого элемента, взятый
с определённым знаком, который определяется
по формуле:

Теорема о понижении порядка определителя
Теорема утверждает, что любой определитель равен сумме по парных произведений всех элементов какой либо строки (столбца) на алгебраические дополнения.
Свойства определителей.
При транспонировании матрицы её определитель не меняется.
При перестановке двух строк определителя, он меняет свой знак, но по абсолютной величине не меняется.
При умножении определителя на число, достаточно умножить любую строку на это число.
Если определитель содержит нулевую строку, то он равен нулю.
Свойство упрощения определителя.
Определитель не изменяется, если к элементам любой его строки прибавить элементы любой другой его строки, предварительно умножив их на одно и тоже любое число.
Сумма определителей, отличающихся одной строкой, равна определителю с теми же элементами, у которого вместо различных строк стоит строка из суммы элементов различных строк.
Если определитель имеет две пропорциональные строки, то он равен нулю.
Сумма попарных произведений элементов кокой либо строки и алгебраических дополнений соответствующих элементов другой строки равна нулю.
Определитель произведения двух квадратных матриц равен произведению их определителей.
Определитель треугольной матрицы равен произведению своих диагональных элементов.
Билет №2. Решение системы линейных алгебраических уравнений методом Жордана Гаусса.
Алгоритм:
В каждом уравнении выделить по одной базисной переменной (со знаком)
Выразить базисные переменные через остальные (свободные).
Выписать общее решение.
Базисная переменная – переменная, которая присутствует только в одном уравнении.
Метод Ж.Гаусса = Метод последовательного исключения
Обычно имеется общее и частное решение.
Если в каждом уравнении нет по базисной переменной, то следует сделать элементарные преобразования.
«КОНКУРС КРАСОТЫ»
КОНКУРС МЕЖДУ СТОЛБЦАМИ
Складываем столбцами и выбираем меньшую переменную (без знаков)
КОНКУРС МЕЖДУ СТРОЧКАМИ
Складываем строчками и выбираем меньшую переменную (без знаков)
Метод последовательного исключения неизвестных заключается в решении системы алгебраических уравнений с одновременным исследованием её на совместность.
Метод реализуется в два этапа:
Прямой ход метода.
Прямой ход метода Гаусса заключается в преобразовании расширенной матрицы коэффициентов системы к ступенчатому виду с помощью элементарных преобразований, то есть как при нахождении ранга матрицы и базисного минора, но только со строками матрицы. При этом само преобразование к ступенчатому виду с помощью нескольких шагов, на каждом из которых исключается одна переменная, то есть обнуляется нижний элемент одного из столбцов.
В результате выполнения нескольких шагов матрица оказывается приведённой к ступенчатому виду. На этом этапе можно определить ранг матрицы и системы.
Если ранг расширенной матрицы равен рангу матрицы коэффициентов, то система считается совместной, в противном случае система не совместна.
Если количество уравнений равно количеству неизвестных, то система имеет единственное решение, если ранг системы меньше числа неизвестных, то количество решений бесконечно.
Обратный ход метода.
Если
решение единственно:

БИЛЕТ №3.
Линейные матричные операции и их свойства.
Операции над матрицами.
Сложение1 – суммой двух матриц А и В одного порядка называют матрицу С того же порядка, каждый элемент которой равен сумме соответствующих элементов двух первых матриц.
Матрицы разных порядков сложению не подлежат.
Умножение матрицы на число: Произведение матрицы и числа – есть матрица того же порядка, каждый элемент которой умножен на число.
Произведение матриц согласованных2 порядков:

Транспонирование – это операция, при которой элементы строк матрицы А становятся элементами столбцов матрицы В.
Свойства линейных операций над матрицами.
А+В=В+А
А+(В+С)=(А+В)+С
а(А+В)=аА+аВ
(а+в)А=аА+вА
а(вА)=(ав)А
(А+В)Т=АТ+ ВТ
А-В=А+(-1)В
А-А=0
Следствие:
(аА+вВ)Т=аАТ+вВТ
Свойства умножения матриц.

АВС=А(ВС)≠(АС)В
А(В+С)=АВ+АС
С(А+В)=СА+СВ
(С+В)А=ВА+СА
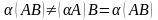

(АВ)Т=ВТАТ
(АТ)Т=А
Замечание:

БИЛЕТ №4.
Произведение матриц. Правило умножения и свойства.
Произведение матриц согласованных3 порядков:
Свойства умножения матриц.
АВС=А(ВС)≠(АС)В
А(В+С)=АВ+АС
С(А+В)=СА+СВ
(С+В)А=ВА+СА
(АВ)Т=ВТАТ
(АТ)Т=А
