Значения степени черноты для некоторых материалов:

Табл.4

Материал	Т,К	
Алюминий: отожжен, электрополирован	300 76 4	0,03 0,018* 0,011
Медь: окисленная поверхность механическая полировка электрополировка	300 4 4	0,78 0.015 0,0062
Золото , =12 мкм	76	0,016*
Золотое покрытие на нержавеющей стали, =5 мкм	76	0,025*
Cеребро, окисленная поверхность	76	0,01*
Латунь : полированная окисленная поверхность	373 300	0.03 0,78
Стекло	293	0,94
Сталь нержавеющая, механическая полировка	76	0,048

*) полусферическая степень черноты.

Выводы:

1. Материалы с наибольшей отражательной способностью (наи- меньшая степень черноты) обладают наименьшим электрическим сопротивлением( медь, серебро, золото, алюминий).

2. С понижением температуры относительная степень черноты уменьшается.

3. Загрязненные поверхности увеличивают степень черноты.

4. Сплавы имеют большую степень черноты , чем чистые металлы.

5. Обработка приводит к уплотнению поверхностного слоя (механическая полировка), увеличивая степень черноты.

Зависимость для определения количества потока лучистой энергии.

Поток лучистой энергии от теплой поверхности с Т_т к холодной с Т_х в непоглащающей и нерассеивающей среде может быть определен по формуле полученной из уравнения Стефана-Больцмена :

Q=_пр F_т [(T_т/100)⁴ - (Т_х/100)⁴] , где

_пр=1/[(1/_т)+F_т /F_х(1/_х-1)],

F_{т , х}- взаимная поверхность излучения.

Определение Q в основном сводится к нахождению F_т,_х зависящей от коэффициента облученности (угловой коэффициент). Вычисление углового коэффициента непростая задача и он может быть вычислен только в простых случаях. Для поверхностей без выпуклости (коаксиальные бесконечно длинные цилиндры, концентрические сферы, сфера с бесконечно тонким диском, расположенном в экваториальной плоскости и др.) на внутренней поверхности угловой коэффициент равен 1 , поэтому F_т,х=F_х.

Повышение эффективности высоковакуумной изоляции .

При давлении не выше 10^-3 Па 90% теплопритока составляет излучение.

Его можно уменьшить установкой непрозрачных экранов.

Р

Т₁Т₂

F₁= F_э=F₂=1

ассмотрим следующий относительно простой пример для плоской системы с одним экраном :

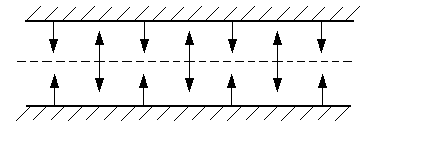
1-теплая поверхность

2-холодная поверхность

Т₁

Экран толщиной δ

Т₂

Тепловое излучение

Рис.12

Допущения:

1. ₁= ₂=_э , ( _1э=_2э) ;

2. /_э0

Требуется найти результирующий тепловой поток Q_э.

Справедлива система уравнений:

Q_1э=_1э[(T₁/100)⁴ - (T_э/100)⁴]

(A)

Q_э2=_э2[(T_э/100)⁴ - (Т₂/100)⁴]

Для стационарного режима Q_1э=Q_2э=Q_э

Из системы (А) находим Т_э

(Т_э/100)⁴ = 0,5[(Т₁/100)⁴+(Т₂/100)⁴]

Подставив это выражение для Т_э снова в уравнение (А) получим

Qэ=0,5₁₂ [ (T₁/100)⁴-(T₂/100)⁴]

Т.е. при наличии одного экрана поток уменьшается в 2 раза .

Для n экранов записывается система из n+1 уравнений типа:

Q_1,э1=_1,э1[(Т₁/100)⁴-(Т_э1/100)⁴]

Q _э1,э2=_э1,э2[(Т_э1/100)⁴-(Т_э2/100)⁴] (Б)

......................................................

Q _эn,2=_эn,2[(Т_эn/100)⁴-(Т₂/100)⁴]

Далее из системы (Б) выразим температурные перепады:

Q_1,э1/_1,э1=(Т₁/100)⁴-(Т_э1/100)

Q_э1,э2/_э1,э2=(Т_э1/100)⁴-(Т_э2/100)⁴

..................................................... (В)

Q _эn,2/_эn,2=(Т_эn/100)⁴-(Т₂/100)⁴

Суммируем уравнения (В) учитывая , что Q_1,э1=Q_э1,э2=...=Q_эn,2. Получаем:

(Q_э/)·(1/_1,э1+1/_э1,2+...+1/_эn,2 )=(T₁/100)⁴-(T₂/100)⁴ ,

тогда Q_э=_1,2(Э) [(T₁/100)⁴-(T₂/100)⁴] ,

где : _1,2(э) =(1/_1,э1+1/_э1,э2+...+1/_эn,2)^-1 =[ 1/_1,2 +(2/_i-1)]^-1

При _1,э1=_э1,э2=...=_эn,2

имеем : Q_э=[1/(n+1)]_1,2 + [(T₁/100)⁴-(T₂/100)⁴]=[1/(n+1)]Q_1,2

Q_э/Q_1,2=1/(n+1)=(n+1)^-1

-отношение результирующих тепловых потоков излучения с экранами и без них. -коэффициент эффективности экранирования. В реальной ситуации _1,2 _э1,э2=_э2,э3=...=_пр.э , тогда для плоских экранов (рис.12):

=[1+n(_1,2/_пр.э)]^-1 ; (Г)

для цилиндрических экранов :

·

={1+(_1,2/_пр.э) [r_x

] }^-1

1

r_x+[1/(n+1)]·( r_т-r_x)

для сферических экранов :

={ 1+_1,2/_пр.э[r_x²

1

] }^-1

r_x+[i/(n+1)]·(r_т-r_x)^-2

Выше приведенные зависимости справедливы для системы n экранов при их одинаковой степени черноты, что допустимо для технических расчетов, а в действительности  понижается с понижением температуры.

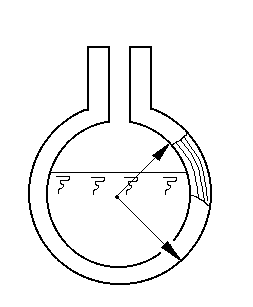
b

Теплая поверхность

Холодная поверхность

Экраны

∆

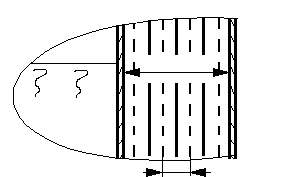
Т_х

прокладки

P≤ 10 ^-3Па

экраны

r₁

Т_т

КЖ

А

КЖ

r₂

Рис.13

нализ уравнения (Г) позволяет сделать следующие выводы :

• При _1,2=_пр.э установка n экранов снижает лучистый поток тепла в (n+1) раз ;

• Особенно эффективно экранирование при _1,2=1 и малых значениях _пр.э. Поток снижается в (1+n/_пр.э)^-1 раз , т.е. в десятки раз .

• При _пр.э=1 и _1,2 1 эффект экранирования не велик и n экранов эквивалентны примерно одному экрану , но полированному:

=(1+n_1,2/_пр.э)^-1 = (1+n_1,2)^-1 1/(1+1)=0,5

(так как n_1,21).