Федеральное агентство по образованию

Российская экономическая академия имени Г.В.Плеханова

Кафедра высшей математики

Лекции по дисциплине «Математический анализ»

Москва 2013

Составители:

канд. физ. матем. наук Р.К. Гринцявичус

Лекции по дисциплине Математический анализ» / Р.К.Гринцявичус. -М.: Изд-во Рос. экон. акад., 2007

Предлагается краткая теория по всем разделам учебной дисциплины «Математический анализ».

Для студентов ОЭФ и факультета МЭО .

§1.Определение предела последовательности

Определение. Перенумерованное множество чисел называется последовательностью.

Последовательность можно задать так называемой формулой -го члена Здесь подразумевается, что

Определение. Последовательность стремится к b при , если для любого существует такое , что для всех справедливо неравенство Коротко это можно записать так: , если

Значок читается «для любого». Значок читается «существует». Значок : читается «такое, что при».

Пример 1.1. Докажем, что

Способ 1. Для заданного возьмем . Тогда из неравенства следует . Отсюда Ч.т.д.

Способ 2. В предыдущем способе не понятно, как мы догадались, что в качестве нужно взять . Это следует из цепочки формул: = .

Способ 3. Нестрогое, но наглядное доказательство следует из таблицы:

	1	10	1000	1000000	100000000000
	2	1,1	1,001	1,000001	1,00000000001

§2. Определение предела функции

Определение. Пусть имеем два множества А и B. Предположим, что каждой точке сопоставлена точка . В этом случае говорят, что задана функция у от х.

Такую функцию обозначают или и так далее.

Примеры: .

Функции можно задать аналитически, графически, таблично.

Частным случаем функции является последовательность

Определение. Число b называется пределом функции при х, стремящемся к а,(обозначается ) если для любого положительного числа существует такое положительное число , что для всех х, не совпадающих с а и удовлетворяющих неравенству выполняется неравенство . Коротко это определение можно записать так: , если .

Замечание. В определении предела мы неявно предполагаем существование такого , что функция определена при любом .

Пример 2.1. Докажем формулу:

Действительно: Рассмотрим цепочку формул: . Теперь ясно, что для заданного положительного нужно взять , ибо из неравенства последует . Ч.т.д.

§3.Функция, стремящаяся к бесконечности

Определение. Функция стремится к бесконечности при х, стремящегося к а, если

.

Пример 3.1. Докажем

Для этого необходимо доказать Убедимся в следующей цепочке формул: . Поэтому для заданного возьмем . Тогда из неравенства последует . Ч.т.д.

Не строгое, но достаточно наглядное доказательство формулы следует из таблицы

	1	0,1	0.001	0.00001
	1	10	1000	100000

Пример 3.2. Рассмотрим графики трех функций :

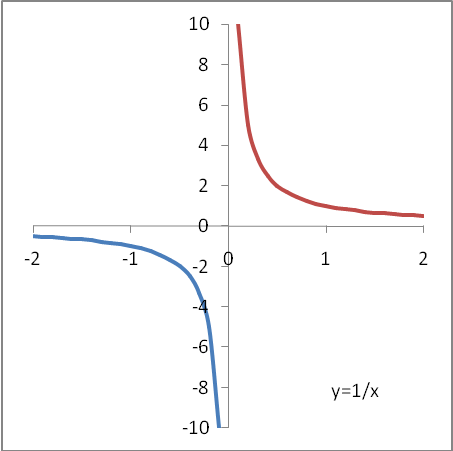
Рис. 3.1 Рис. 3.2 Рис. 3.3

Из этих рисунков можно догадаться в справедливости формул:

.

Замечание 3.1. Знак означает, что х стремится к 0, оставаясь все время больше нуля. Аналогично, означает, что х стремится к 2, оставаясь все время больше двух.

Замечание 3.2. означает, что В этом можно убедиться из рис. 3.2.

Замечание 3.3. Мы часто будем говорить, что 1/0 не существует в том смысле, что оно равняется бесконечности.

Пример 3.3. Для построения графиков необходимо привлекать современные компьютеры. В этом пособии приведены графики, построенные в Еxcel. Например, график (рис. 3.1) в Еxcel можно построить следующим образом:

1) в ячейку А1 вводим число -2;

2) в ячейке А2 программируем формулу =А1+0,1;

3) содержимое ячейки А2 растягиваем вплоть до ячейки А41; в ячейке А41 появиться число 2;

4) в ячейке В1 программируем =1/А1;

5) содержимое ячейки В1 растягиваем вплоть до ячейки В41;

6) ЛК(левой кнопкой мыши) выделяем содержимое ячеек А1:В20;

7) ЛК по Вставка;

8) ЛК по Точечная;

9) ЛК по выбранному типу графика;

10) ПК (правой кнопкой мыши) по графику;

11) ЛК по Выбрать данные;

12) ЛК по Добавить;

13) ЛК по полю Значения Х:;

14) ЛК выделяешь содержимое ячеек А2:А41;

15) ЛК по полю Значения У: и стираешь содержимое этого поля;

16) ЛК выделяешь содержимое ячеек В22:В41;

17) ЛК по ОК;

18) ЛК по ОК.

Пример 3.4. Чтобы график из Еxcel перенести а Уорд, нужно:

1) ЛК по графику;

2) ЛК по знаку меню Копировать;

3) ПК в том месте листа Уорда, где предполагаете вставить график;

4) ЛК по Вставить.