1) Непнерииальные системы отсчета (нсо)

Определение: Неинерпиальной системой отсчета (НСО) называется система, движущаяся ускоренно относительно инерцнальной (ИСО). Простейшие НСО - это системы, движущиеся ускоренно прямолинейно, и системы врашаюшиеся. Задача состоит в том. чтобы найти уравнения движения в НСО. эта задача сводится к установлению законов преобразования сил и ускорений при переходе от ИСО к НСО

Условимся считать произвольно выбранную ИСО неподвижной, а движение относительно нее абсолютным. Если тело неподвижно в системе отсчета, которая движется относительно выбранной ИСО. то такое движение тела назовем переносным.

Движение тела относительно движущейся системы отсчета назовем относительным.

Работа силы тяжести численно равна произведению силы тяжести на вертикальное перемещение точки ее приложения, не зависит от траектории перемещения, а только от расстояние между вертикальными проекциями начального и конечного положения точки:

Общее уравнение динамики. Принцип Д’Аламбера-Лагранжа.

Принцип Д’Аламбера: (P_i + R_i + Ф_i) = 0; (P_i + R_i + Ф_i)r_i = 0, полагаем. что связи, наложенные на механическую систему двисторонние, стационарные, голономные и идеальные, тогда: (R_i  r_i) = 0;

(P_i + Ф_i)r_i = 0 - общее уравнение динамики - для движения механической системы с двусторонними, стационарными, голономными и идеальными связями сумма работ задаваемых сил и сил инерции точек системы на любом возможном перемещении равна нулю.

Билет 18.

Импульс силы - векторная величина, характеризующая передачу материальной точке механического движения за некоторый промежуток времени со стороны других тел, действующих на нее, равна произведению силы на время ее действия и совпадает с ней по направлению: ; В проекциях на оси:

Теорема об изменении количества движения материальной точки.

Количество движения материальной точки - вектор, численно равный произведению массы точки на скорость ее движения и совпадающий с ней по направлению.

Основное уравнение динамики: ; . Интегрируя получим: ; .

Теорема: Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку за этот промежуток времени.

Вынужденные колебания без учета сопротивления среды

Такие колебания происходят, если на точку, кроме восстанавливающей силы действует вынуждающая сила, изменяющаяся по гармоническому закону: H

Вынужденные колебания с учетом сопротивления среды

Такие колебания происходят, если на точку, кроме восстанавливающей и вынуждающей силы действует сила сопротивления:

R=-µv µ - коэффициент сопротивления среды

2) Кинетический момент относительно полюса - главный момент количества движения механической системы относительно полюса - вектор, равный геометрической сумме момента количества движения всех точек системы относительно того же полюса:

Кинетический момент относительно оси - скаляр, равный алгебраической сумме моментов количеств движения всех точек системы относительно той же оси:

Кинетический момент вращающегося твердого тела относительно оси вращения равен произведению угловой скорости на момент инерции тела относительно оси вращения: ; .

В механике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел.Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных.

Билет 19

Кинетическая энергия механической системы - скаляр, равный сумме кинетических энергий всех точек системы: .

При поступательном движении:

При вращательном движении:

При плоскопараллельном движении: , где d - расстояние от центра масс до МЦС

Теорема Кёнига

Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.

Формулировка: Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где T — полная кинетическая энергия, — энергия движения центра масс, — относительная кинетическая энергия.

Моменты инерции твердого тела. Радиус инерции.

Момент инерции - скалярная величина, равная произведению массы на квадрат расстояния.

Планарный момент инерции - момент инерции относительно плоскости: ; осевой - относительно оси: ; полярный - относительно полюса: ; центробежный момент инерции: .

Радиус инерции - расстояние от оси до воображаемой точки, в которой необходимо сосредоточить массу тела, чтоб момент инерции этой точки относительно заданной оси был равен моменту инерции данного тела относительно этой же оси: .

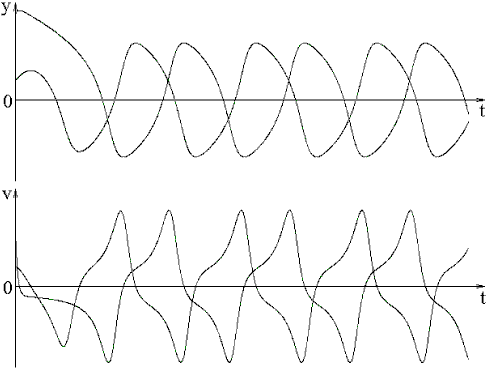
Автоколебаниями называют любые гармонические колебания, причиной которых является непериодическая сила с любым временем действия.

2) Дифференциальные уравнения вращательного движения твердого тела.

. Аналогично для двух других осей:

Задачи:

1. по закону движения и моменту инерции определить главный вектор момент всех внешних сил, действующих на точки данного тела.

2. по внешним силам, моментам инерции и начальным условиям найти закон движения тела.

3. по внешним силам и угловому ускорению определить момент инерции.

Дифференциальные уравнения плоскопараллельного движения твердого тела.

Плоскопараллельное движение состоит из поступательного вместе с центром масс и вращательного вокруг него: